Introduction to Boyle’s Law
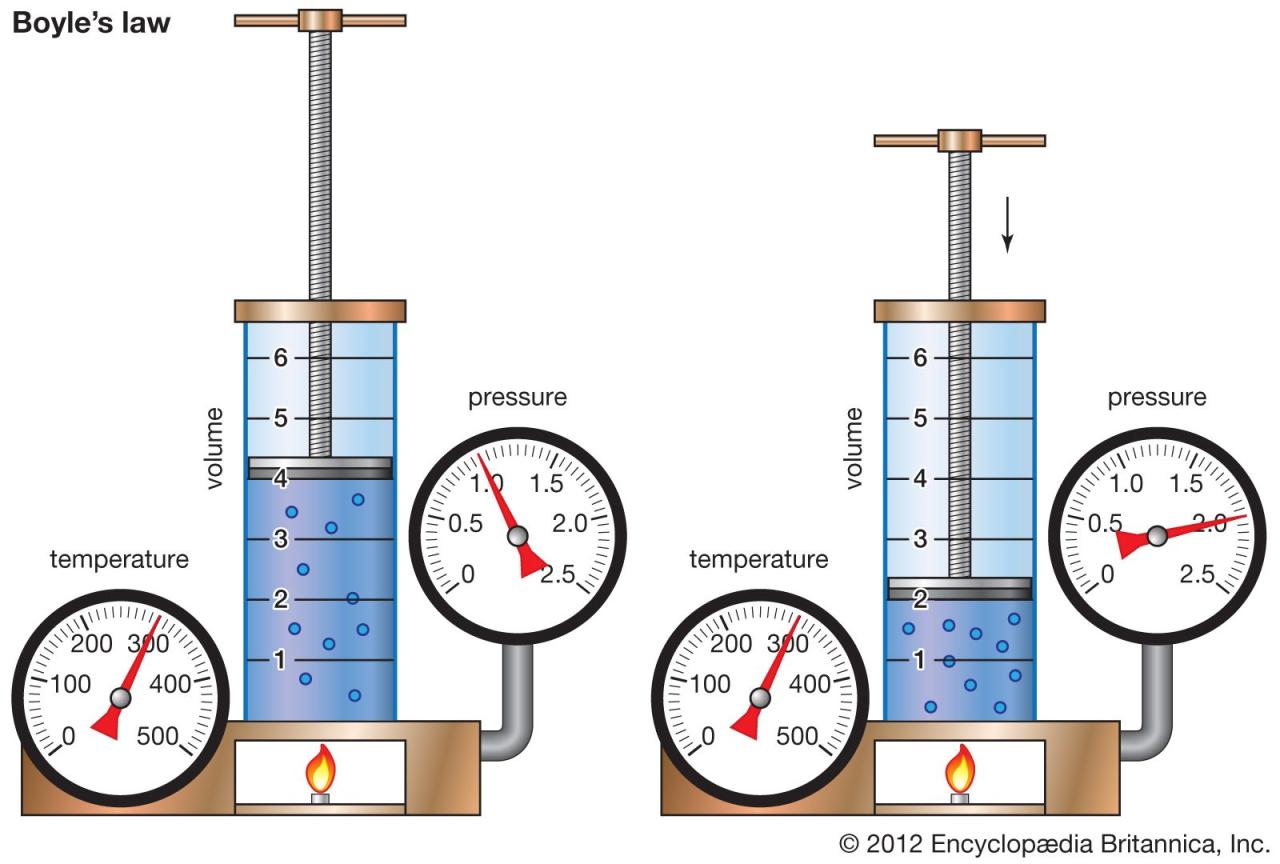
Boyle’s Law is a fundamental principle in physics that describes the inverse relationship between the pressure and volume of a gas, provided the temperature and the amount of gas remain constant. In simpler terms, if you squeeze a gas into a smaller space (decreasing its volume), its pressure will increase. Conversely, if you allow the gas to expand (increasing its volume), its pressure will decrease. This relationship is crucial for understanding the behavior of gases in various contexts.
Boyle’s Law, while bearing his name, wasn’t solely discovered by Robert Boyle. Early observations of the pressure-volume relationship were made by others, but Boyle, in 1662, conducted meticulous experiments using a J-shaped tube and mercury to quantify this relationship precisely. He documented the inverse proportionality between pressure and volume, a finding that significantly advanced our understanding of gases and laid the groundwork for future developments in thermodynamics and chemistry. His work highlighted the importance of controlled experimentation and quantitative analysis in scientific discovery, establishing a model for future scientific investigation. The significance of Boyle’s Law extends far beyond its initial application; it serves as a cornerstone of the ideal gas law and provides a crucial framework for understanding the behavior of gases in a wide array of applications.
Real-World Applications of Boyle’s Law
Boyle’s Law is not just a theoretical concept; it has numerous practical applications in our daily lives and various industries. Understanding this inverse relationship between pressure and volume is essential for designing and operating many systems and devices.
| Example | Description | Pressure Changes | Volume Changes |
|---|---|---|---|
| Inflatable Balloons | As you blow air into a balloon, you increase the amount of gas inside, thus increasing the pressure. This increased pressure expands the balloon’s volume. Conversely, when the air is released, the pressure decreases, causing the volume to decrease. | Increases then decreases | Increases then decreases |
| Scuba Diving | At greater depths, the pressure of the water increases significantly. This increased pressure compresses the air in a diver’s lungs, reducing their volume. As divers ascend, the pressure decreases, allowing the air volume to expand. This is why divers must ascend slowly to avoid potentially dangerous expansion of air in their lungs. | Increases with depth, decreases with ascent | Decreases with depth, increases with ascent |
| Pneumatic Systems | Pneumatic tools and systems, such as air brakes in vehicles, utilize compressed air. The compressed air stores potential energy, and its release controls the operation of the system. The pressure of the compressed air is inversely related to the volume of the air reservoir. | High initial pressure, decreases during operation | Decreases as air is released |
| Medical Ventilators | Medical ventilators use Boyle’s Law to deliver air to patients’ lungs. The machine alters pressure to control the volume of air delivered, assisting patients with breathing difficulties. Precise control of pressure and volume is crucial for effective ventilation. | Adjusted to control airflow and lung volume | Adjusted to control airflow and lung volume |
Mathematical Representation of Boyle’s Law: What Are The Varibles For Boyles Law
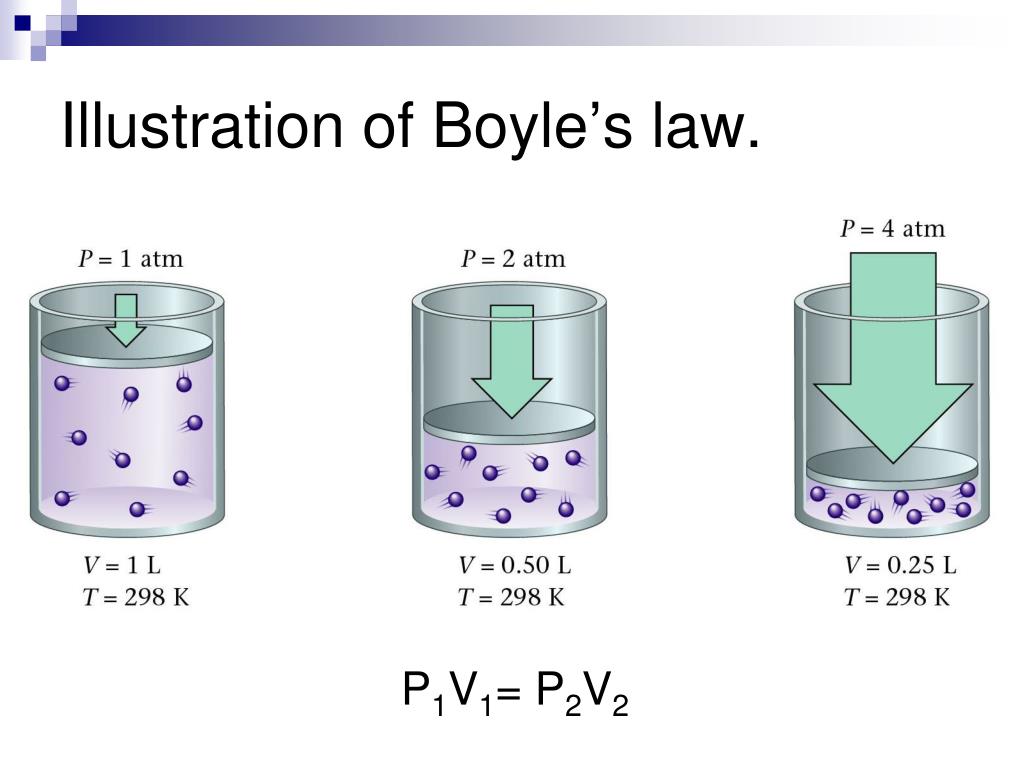
Boyle’s Law, describing the inverse relationship between pressure and volume of a gas under constant temperature, is elegantly summarized by a concise mathematical formula. This formula allows for precise calculations of how changes in one variable affect the other. Understanding this formula is crucial for applying Boyle’s Law in various scientific and engineering applications.
The fundamental equation representing Boyle’s Law is:
P1V1 = P2V2
Here, P1 represents the initial pressure of the gas, and V1 represents its initial volume. Similarly, P2 and V2 represent the final pressure and volume of the gas, respectively, after a change has occurred. It’s important to remember that this equation holds true only when the temperature and the amount of gas remain constant throughout the process.
Example Problems and Solutions
The following examples demonstrate how to utilize the Boyle’s Law formula to solve problems involving changes in pressure and volume of a gas. Consistent units are essential for accurate calculations; ensure pressure and volume units are consistent throughout each problem.
| Problem | Steps to Solve | Solution | Result |
|---|---|---|---|
| A gas occupies 5.0 L at a pressure of 1.0 atm. If the pressure is increased to 2.5 atm at constant temperature, what is the new volume? | 1. Identify known variables: P1 = 1.0 atm, V1 = 5.0 L, P2 = 2.5 atm. 2. Solve for V2 using the formula: V2 = (P1V1)/P2 3. Substitute known values and calculate. |
V2 = (1.0 atm * 5.0 L) / 2.5 atm = 2.0 L | The new volume is 2.0 L. |
| A balloon filled with helium has a volume of 2.5 L at a pressure of 1.2 atm. If the balloon is compressed to a volume of 1.0 L at constant temperature, what is the new pressure? | 1. Identify known variables: V1 = 2.5 L, P1 = 1.2 atm, V2 = 1.0 L 2. Solve for P2 using the formula: P2 = (P1V1)/V2 3. Substitute known values and calculate. |
P2 = (1.2 atm * 2.5 L) / 1.0 L = 3.0 atm | The new pressure is 3.0 atm. |
| A sample of gas has a volume of 100 mL at a pressure of 760 mmHg. What will be the volume if the pressure is reduced to 380 mmHg at constant temperature? | 1. Identify known variables: V1 = 100 mL, P1 = 760 mmHg, P2 = 380 mmHg 2. Solve for V2 using the formula: V2 = (P1V1)/P2 3. Substitute known values and calculate. |
V2 = (760 mmHg * 100 mL) / 380 mmHg = 200 mL | The new volume is 200 mL. |
| A scuba tank contains 12 L of air at 200 atm. If the air is released to a pressure of 1 atm at constant temperature, what will be the volume of the expanded air? (Assume ideal gas behavior) | 1. Identify known variables: V1 = 12 L, P1 = 200 atm, P2 = 1 atm 2. Solve for V2 using the formula: V2 = (P1V1)/P2 3. Substitute known values and calculate. |
V2 = (200 atm * 12 L) / 1 atm = 2400 L | The expanded air will occupy 2400 L. |
Limitations and Ideal Gas Assumptions

Boyle’s Law, while a fundamental principle in chemistry, is not a universally applicable model for gas behavior. Its accuracy is contingent upon several assumptions about the nature of the gas itself, and deviations from these assumptions lead to limitations in its predictive power. Understanding these limitations is crucial for applying Boyle’s Law appropriately and recognizing when more sophisticated models are necessary.
Boyle’s Law assumes ideal gas behavior. This means the gas particles are considered to be point masses with negligible volume, and the interactions between them (attractive or repulsive forces) are insignificant. These assumptions simplify the mathematical description of gas behavior, making Boyle’s Law relatively straightforward. However, real gases deviate from this ideal behavior, particularly at high pressures and low temperatures.
Ideal Gas Assumptions and Their Implications
The ideal gas assumptions underpinning Boyle’s Law are critical to its simplicity and applicability within certain limits. The assumption of negligible particle volume implies that the space occupied by the gas molecules themselves is insignificant compared to the total volume of the container. This is a reasonable approximation at low pressures where the molecules are far apart. However, at high pressures, the volume occupied by the molecules becomes a significant fraction of the total volume, leading to deviations from Boyle’s Law. Similarly, the assumption of negligible intermolecular forces is valid when the molecules are far apart and their interactions are weak. At low temperatures, however, intermolecular attractive forces become more significant, causing the gas to deviate from ideal behavior. These attractive forces cause the gas to be more compressible than predicted by Boyle’s Law.
Comparison with the Ideal Gas Law, What are the varibles for boyles law
Boyle’s Law, which states that the product of pressure and volume is constant at a constant temperature (PV = k at constant T), is a special case of the more general Ideal Gas Law: PV = nRT. Here, ‘n’ represents the number of moles of gas, and ‘R’ is the ideal gas constant. The Ideal Gas Law accounts for the amount of gas present, allowing for a more comprehensive description of gas behavior under varying conditions. Boyle’s Law can be derived from the Ideal Gas Law by holding the temperature (T) and the number of moles (n) constant. Therefore, the Ideal Gas Law provides a more complete and accurate description of gas behavior than Boyle’s Law, especially when dealing with situations where the temperature or the amount of gas changes. The Ideal Gas Law provides a better approximation of real gas behavior than Boyle’s Law, particularly at higher pressures and lower temperatures, where the assumptions of negligible particle volume and intermolecular forces become less valid. Real gases, especially those with strong intermolecular forces, may deviate significantly from both Boyle’s Law and the Ideal Gas Law, requiring more complex equations of state for accurate modeling.

Tim Redaksi