Which Variable Will Be Constant in Charles Law?

Introduction to Charles’s Law

Charles’s Law describes the relationship between the volume and temperature of a gas when the pressure and the amount of gas are kept constant. In simpler terms, it states that as the temperature of a gas increases, its volume will also increase proportionally, and vice versa, assuming the pressure remains unchanged. This relationship is particularly useful in understanding the behavior of gases under varying temperature conditions.

Charles’s Law is a fundamental gas law that helps us predict how gases will behave under different conditions. Understanding this relationship is crucial in various fields, from meteorology to engineering.

Mathematical Expression of Charles’s Law

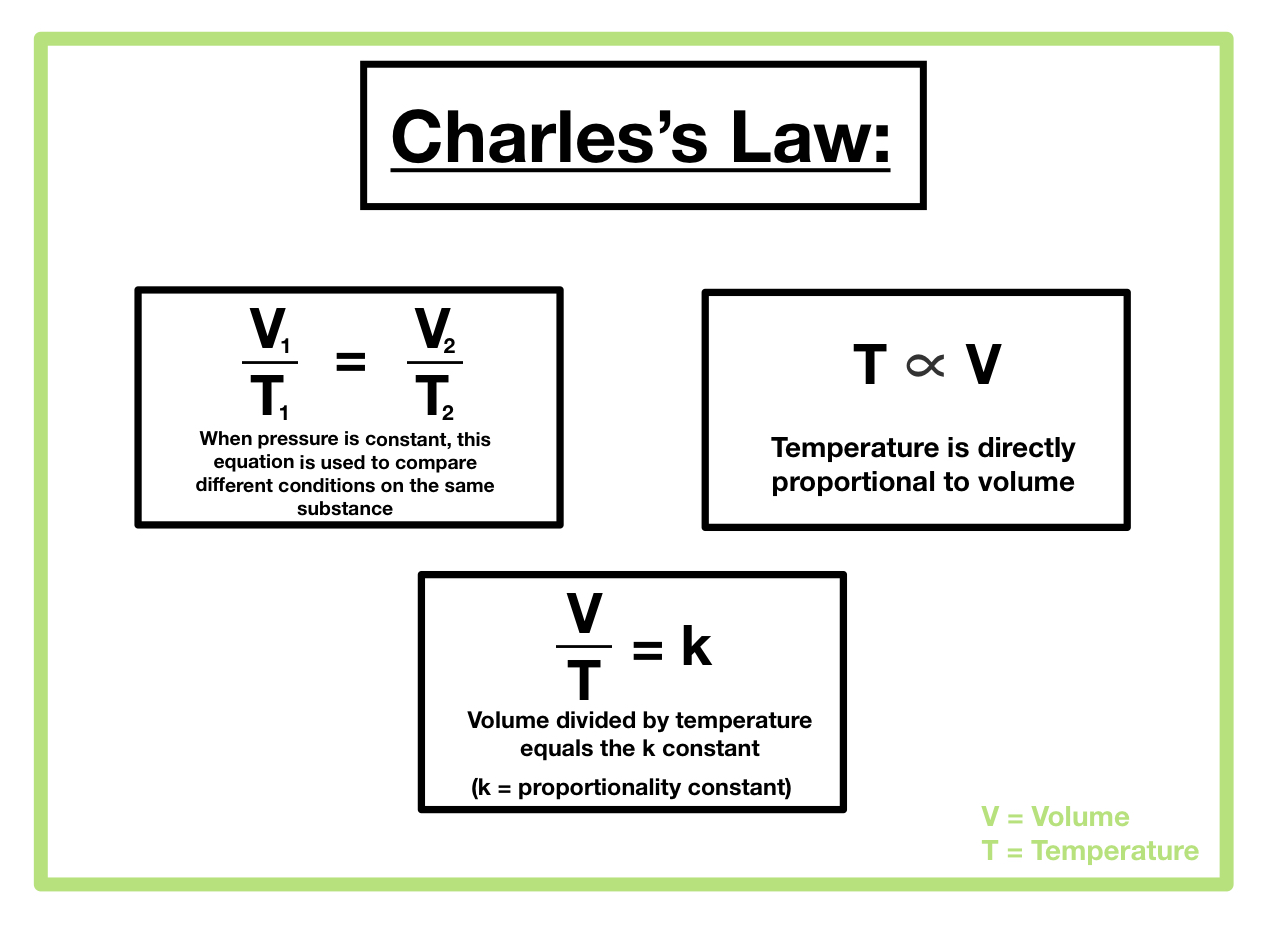
Charles’s Law can be concisely expressed mathematically. The ratio of the volume of a gas to its absolute temperature remains constant, provided the pressure and amount of gas remain constant. This can be written as:

V₁/T₁ = V₂/T₂

Where:

* V₁ represents the initial volume of the gas
* T₁ represents the initial absolute temperature of the gas (in Kelvin)
* V₂ represents the final volume of the gas
* T₂ represents the final absolute temperature of the gas (in Kelvin)

It’s crucial to remember that temperature must always be expressed in Kelvin (K) for this equation to work correctly. Kelvin is the absolute temperature scale, where 0 K represents absolute zero, the theoretical point at which all molecular motion ceases.

Real-World Example of Charles’s Law

A hot air balloon provides a clear illustration of Charles’s Law in action. The air inside the balloon is heated using a burner. As the air heats up, its volume increases, making the balloon less dense than the surrounding cooler air. This difference in density creates buoyant force, causing the balloon to rise. Conversely, as the air inside the balloon cools, its volume decreases, and the balloon descends. The constant pressure exerted by the surrounding atmosphere allows for a direct observation of the volume-temperature relationship predicted by Charles’s Law. The balloon’s ascent and descent are direct consequences of the volume changes caused by temperature variations.

Applications of Charles’s Law: Which Variable Will Be Constant In In Charles Law

Charles’s Law, while a fundamental principle of physics, finds numerous practical applications in various fields. Understanding its implications is crucial for designing and operating systems where temperature changes significantly affect gas volume. From everyday appliances to sophisticated industrial processes, the law’s impact is widespread.

Which variable will be constant in in charles law – The relationship between temperature and volume of a gas, as described by Charles’s Law, is exploited in numerous ways. Its predictable nature allows for precise calculations and engineering designs, minimizing risks associated with thermal expansion and contraction.

Hot Air Balloons

Hot air balloons provide a visually striking example of Charles’s Law in action. Heating the air inside the balloon reduces its density, causing it to rise due to buoyancy. The increased temperature directly correlates with the expansion of the air, increasing the balloon’s volume and lifting capacity. Pilots carefully control the burner to adjust the temperature and thus the altitude of the balloon, demonstrating a direct application of the law. The precise amount of heating required to achieve a specific altitude is calculated using principles derived from Charles’s Law.

Weather Forecasting

Meteorologists utilize Charles’s Law to understand and predict weather patterns. Changes in atmospheric temperature directly influence air volume, impacting pressure systems and ultimately, weather conditions. For example, understanding how temperature changes affect the volume of air masses is critical for predicting the formation and movement of storms and fronts. Accurate weather forecasting relies heavily on the ability to model these thermal effects using principles based on Charles’s Law.

Tire Pressure, Which variable will be constant in in charles law

The pressure in car tires increases on hot days due to the expansion of the air inside. This expansion, a direct consequence of Charles’s Law, highlights the importance of maintaining proper tire pressure. Over-inflation can lead to tire blowouts, while under-inflation reduces fuel efficiency and tire life. Understanding this relationship between temperature and volume allows drivers to adjust tire pressure appropriately based on ambient temperature, ensuring safe and efficient driving.

Refrigeration and Air Conditioning

Refrigeration and air conditioning systems rely heavily on the principles of Charles’s Law. These systems manipulate the volume and pressure of refrigerants to achieve cooling. The expansion and compression cycles involve significant temperature changes, directly impacting the volume of the refrigerant. Understanding these volume changes is crucial for designing efficient and effective cooling systems. The precise calculations involved in the design of these systems are based on the quantitative relationships described by Charles’s Law.

Limitations of Charles’s Law

Charles’s Law, while a valuable simplification of gas behavior, holds true only under specific conditions. It’s a crucial stepping stone in understanding ideal gases, but real-world gases exhibit deviations, particularly under extreme conditions. Understanding these limitations is essential for accurate predictions and applications.

Charles’s Law assumes an ideal gas, meaning the gas particles have negligible volume and no intermolecular forces. These assumptions break down at high pressures and low temperatures where the gas molecules are closer together and intermolecular forces become significant. Additionally, the law’s accuracy is dependent on the nature of the gas itself; some gases deviate more significantly than others.

Deviations at Extreme Temperatures and Pressures

At extremely low temperatures, gases approach their liquefaction point. Intermolecular attractive forces become dominant, causing significant deviations from the predicted volume-temperature relationship. For example, consider trying to apply Charles’s Law to helium near its boiling point (around 4 Kelvin). The volume will not decrease linearly with temperature as predicted, because the attractive forces between helium atoms become significant at this low temperature. Conversely, at extremely high pressures, the volume occupied by the gas molecules themselves becomes a non-negligible fraction of the total volume. This means the assumption of negligible molecular volume in the ideal gas model is no longer valid. The gas’s compressibility factor deviates from unity, leading to a non-linear relationship between volume and temperature. For instance, applying Charles’s Law to a gas compressed to hundreds of atmospheres would lead to inaccurate volume predictions.

Comparison of Charles’s Law and the Ideal Gas Law

Charles’s Law is a special case of the more general Ideal Gas Law. The Ideal Gas Law, represented as

PV = nRT

, where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is temperature, describes the behavior of ideal gases under a wider range of conditions. Charles’s Law, which states that the volume of a gas is directly proportional to its absolute temperature at constant pressure (

V/T = k, where k is a constant

), can be derived from the Ideal Gas Law by holding pressure and the number of moles constant. The key difference lies in the scope: Charles’s Law applies only under constant pressure and a fixed amount of gas, while the Ideal Gas Law accounts for variations in pressure, volume, temperature, and the amount of gas. Therefore, the Ideal Gas Law provides a more comprehensive and accurate description of gas behavior across a wider range of conditions than Charles’s Law.