Mathematical Representation of Centripetal Force
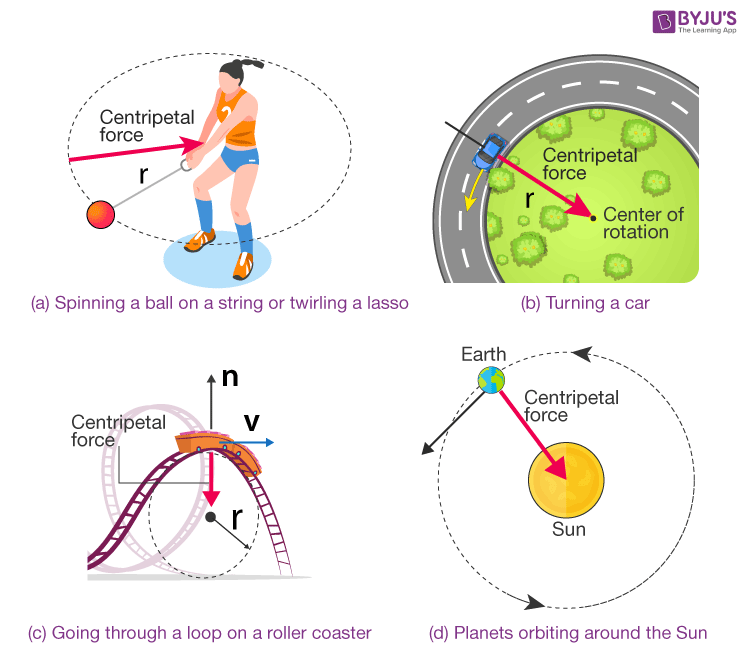
Centripetal force, the force that keeps an object moving in a circular path, can be precisely described using a mathematical formula. Understanding this formula allows us to calculate the force required to maintain circular motion under various conditions, from a car navigating a curve to a planet orbiting a star. This section will delve into the formula itself, explain its components, and illustrate its application through a practical example.
The formula for calculating centripetal force is a fundamental concept in physics. It elegantly connects the object’s mass, velocity, and the radius of its circular path to the force required to maintain that motion.
Centripetal Force Formula and Variables
The centripetal force (Fc) is calculated using the following formula:
Fc = mv²/r
Where:
* Fc represents the centripetal force, measured in Newtons (N). This is the force directed towards the center of the circle, responsible for the change in direction of the object’s velocity.
* m represents the mass of the object, measured in kilograms (kg). A larger mass requires a greater centripetal force to maintain the same circular motion.
* v represents the velocity (speed) of the object, measured in meters per second (m/s). A higher velocity necessitates a stronger centripetal force to keep the object on its circular path.
* r represents the radius of the circular path, measured in meters (m). A smaller radius requires a larger centripetal force for the same velocity.
Example Calculation of Centripetal Force, What law of motion does centripetal force use
Let’s consider a simple scenario: a 1000 kg car traveling at 20 m/s around a curve with a radius of 50 meters. We can use the formula to calculate the centripetal force acting on the car.
Step-by-step solution:
1. Identify the known variables:
* m = 1000 kg
* v = 20 m/s
* r = 50 m
2. Substitute the values into the formula:
Fc = (1000 kg)(20 m/s)² / 50 m
3. Calculate the centripetal force:
Fc = (1000 kg)(400 m²/s²) / 50 m = 8000 N
Therefore, the centripetal force required to keep the car moving in a circle is 8000 Newtons. This force is provided by the friction between the tires and the road surface.
Steps in Solving Centripetal Force Problems
Solving problems involving centripetal force often involves a systematic approach. A clear understanding of the formula and the variables involved is crucial. The following steps Artikel a general procedure:
* Identify the knowns and unknowns: Carefully examine the problem statement to determine which variables (mass, velocity, radius, and centripetal force) are given and which need to be calculated.
* Select the appropriate formula: Use the centripetal force formula (Fc = mv²/r).
* Substitute the known values: Carefully substitute the numerical values of the known variables into the formula, ensuring consistent units.
* Perform the calculation: Calculate the value of the unknown variable using the appropriate mathematical operations. Pay attention to units throughout the calculation.
* State the answer with units: Always express the final answer with the correct units (Newtons for force).
Centrifugal Force (as a contrast): What Law Of Motion Does Centripetal Force Use
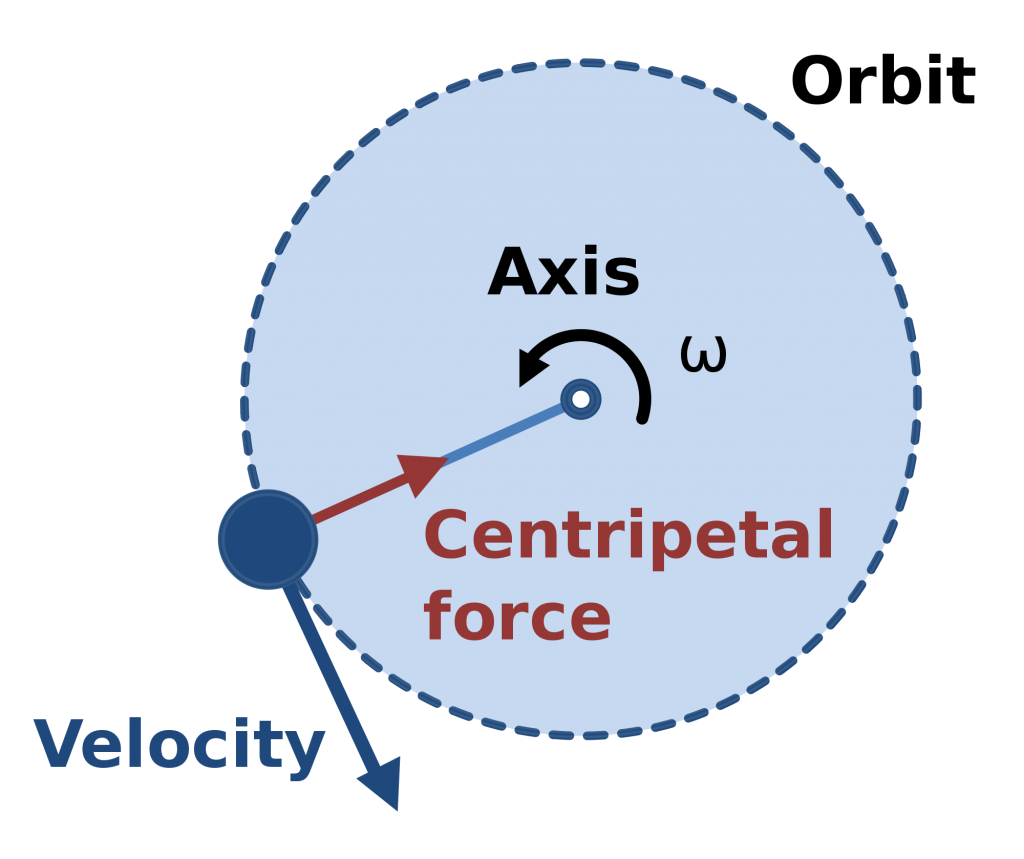
Centrifugal force, often mistakenly described as a force pulling outwards, is fundamentally different from centripetal force. While centripetal force is a real force causing inward acceleration, centrifugal force is an apparent force experienced in a rotating frame of reference. Understanding this distinction requires analyzing the forces from different perspectives.
Centripetal force, as previously discussed, is the force that keeps an object moving in a circular path. It always acts towards the center of the circle. In contrast, centrifugal force is an inertial force; it’s not a real force acting on the object itself, but rather a perceived outward force arising from the object’s inertia resisting the change in direction imposed by the centripetal force. Imagine spinning a ball on a string: the centripetal force is the tension in the string pulling the ball inwards, preventing it from flying off. From the perspective of someone rotating with the ball (a non-inertial frame of reference), it appears as if a force is pushing the ball outwards, this is the centrifugal force.
Centrifugal Force as a Fictitious Force
Centrifugal force is classified as a fictitious force, also known as an inertial force or pseudo-force. It’s not a real force in the sense that it doesn’t arise from an interaction with another object. Instead, it’s a consequence of observing motion from a non-inertial (accelerating) frame of reference. Newton’s laws of motion only apply accurately in inertial frames – frames that are not accelerating. When we analyze the rotating ball from a stationary (inertial) frame, we only see the centripetal force. The outward “push” is simply the ball’s tendency to continue moving in a straight line (due to inertia), a tendency counteracted by the centripetal force.
Frames of Reference and Force Observation
The observation of centripetal and centrifugal forces is entirely dependent on the frame of reference.
In an inertial frame of reference (a frame not accelerating), only the centripetal force is observed. For example, an observer standing still watching the spinning ball would only see the tension in the string (centripetal force) pulling the ball inward.
In a non-inertial frame of reference (a frame that is accelerating), both centripetal and centrifugal forces are observed. An observer rotating with the ball would feel themselves being pushed outwards, experiencing the centrifugal force. They would also observe the inward pull of the string (centripetal force), but the outward force would appear to balance it, maintaining the ball’s position relative to them. This apparent balance is why centrifugal force is often misinterpreted as a “real” force. A classic example of this is the feeling of being pushed outwards when riding a carousel. The sensation of being “pushed” is the centrifugal force, a consequence of observing the motion from a rotating (non-inertial) frame.

Tim Redaksi