Mathematical Constraints: When Can Yiu Not Use Law Of Sins
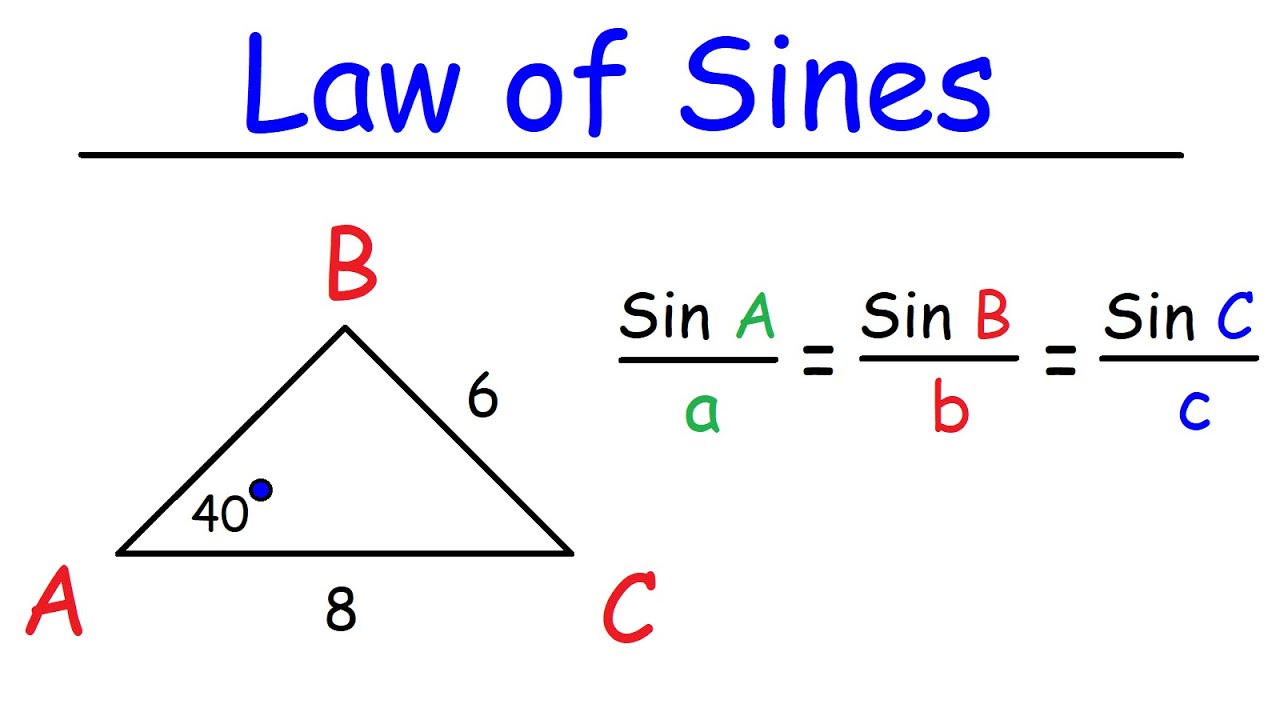
The Law of Sines, a powerful tool in trigonometry, elegantly connects the angles and sides of any triangle. However, its application isn’t without limitations. A crucial constraint stems from the mathematical operations involved, specifically the potential for division by zero. Understanding and mitigating this risk is essential for accurate and reliable results.
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is constant for all three sides. This is expressed as: a/sin A = b/sin B = c/sin C, where a, b, and c are the lengths of the sides and A, B, and C are the angles opposite those sides respectively. Division by zero occurs when the sine of an angle in the denominator is equal to zero. Since sin(0°) = sin(180°) = 0, this situation arises when one of the angles in the triangle is either 0° or 180°.
Division by Zero Scenarios in Triangle Configurations
A triangle with an angle of 0° or 180° is degenerate; it’s not a true triangle in the geometric sense. Consider a triangle where angle A is 0°. This means sides a and b would overlap, collapsing the triangle into a straight line. Applying the Law of Sines would involve dividing by sin(0°), which is zero, resulting in an undefined result. Similarly, if angle A were 180°, sides b and c would overlap, again forming a straight line, and division by sin(180°) would also lead to a division by zero error. Another example would be attempting to solve a triangle where two angles sum to 180°. This would imply the third angle is 0°, leading to the same problem.
Flowchart for Avoiding Division by Zero Errors
Before applying the Law of Sines, it is crucial to check for potential division by zero errors. The following flowchart Artikels the steps:
[Imagine a flowchart here. The flowchart would begin with a rectangle labeled “Start”. An arrow would lead to a diamond-shaped decision box labeled “Is any angle in the triangle 0° or 180°?”. If yes, an arrow leads to a rectangle labeled “Division by zero error; Law of Sines cannot be applied”. If no, an arrow leads to a rectangle labeled “Apply Law of Sines”. Finally, an arrow leads from both rectangles to a rectangle labeled “End”.]
The flowchart visually represents the decision-making process. By systematically checking for angles of 0° or 180°, one can prevent the application of the Law of Sines in scenarios where it would lead to a division by zero error, ensuring accurate calculations. Note that the ambiguous case of the Law of Sines (where two solutions are possible) does not directly involve division by zero, but rather the possibility of multiple triangles satisfying the given conditions. This is a different issue from the division by zero error.
Practical Applications and Limitations
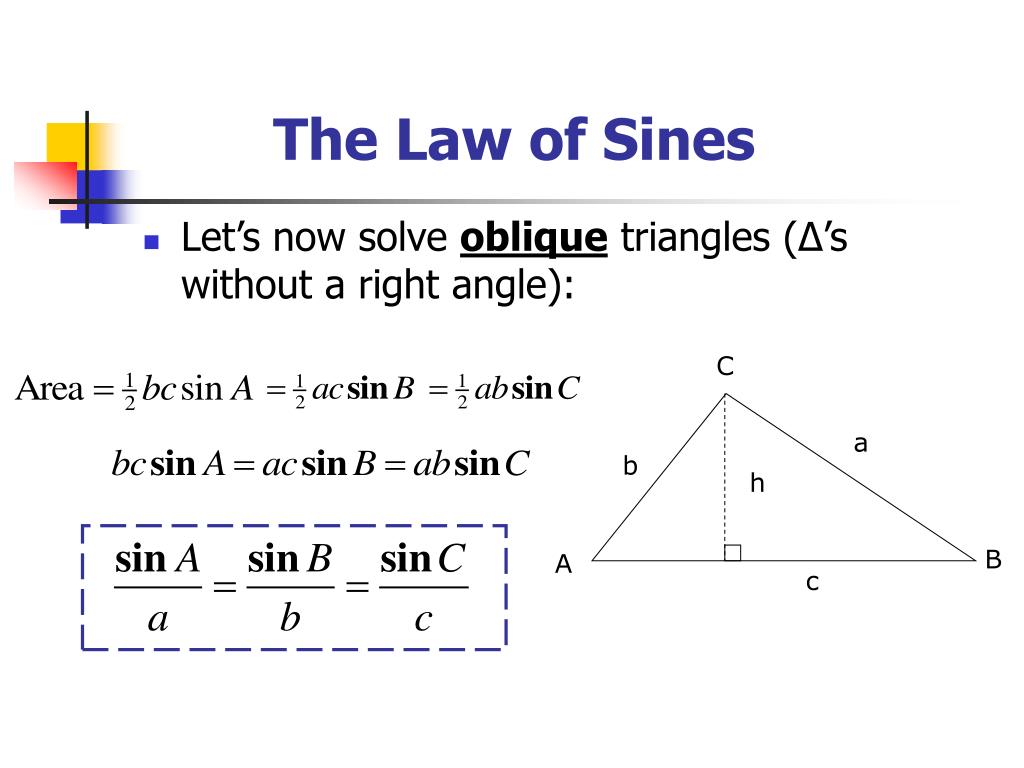
The Law of Sines, while a powerful tool in trigonometry, is not universally applicable. Its effectiveness hinges on specific conditions within a given problem, and understanding these limitations is crucial for choosing the appropriate mathematical approach. This section explores the practical applications and limitations of the Law of Sines, contrasting it with the Law of Cosines and providing examples of its suitable and unsuitable applications.
A Real-World Problem Where the Law of Sines Is Inappropriate
Consider the task of determining the distance between two points, A and B, located on opposite sides of a wide river. We can measure the distance from point A to a point C on the same side of the river as A (let’s say 100 meters). We can also measure the angles ∠BAC (let’s say 70 degrees) and ∠BCA (let’s say 80 degrees). It seems we have two angles and a side, a classic scenario for the Law of Sines. However, the Law of Sines would be ineffective here because it requires at least one known angle-side pair, where the angle and side are opposite each other. While we know the angle at C and the side opposite it is AB (the distance we want to find), we do not know the length of the side AC, nor the angle at B. The Law of Sines cannot be directly applied without additional information. The most appropriate approach here would be to utilize the Law of Cosines to solve for AB, after calculating angle A.
Comparison of the Law of Sines and the Law of Cosines, When can yiu not use law of sins
The Law of Sines and the Law of Cosines both address problems involving triangles, but they excel in different situations. The following table highlights their strengths and weaknesses:
| Feature | Law of Sines | Law of Cosines |
|---|---|---|
| Strengths | Efficient for solving triangles when you know two angles and one side (AAS, ASA) or two sides and an angle opposite one of them (SSA, but ambiguous case possible). | Effective when you know three sides (SSS) or two sides and the included angle (SAS). Can directly solve for any side or angle. |
| Weaknesses | Ambiguous case in SSA scenarios; ineffective when only three sides are known or two sides and the included angle are known. | More complex calculations compared to the Law of Sines, particularly when solving for angles. |
Real-World Scenarios: Suitable Applications of the Law of Sines
The Law of Sines is a practical tool in various situations. For instance, it is frequently used in surveying to determine distances and angles across difficult terrain, such as determining the width of a canyon using angles and a measurable distance. It also finds application in navigation, particularly in aerial or maritime navigation, for calculating distances and bearings based on observed angles and known distances. In astronomy, it assists in calculating distances between celestial bodies based on angular measurements.
Real-World Scenarios: Unsuitable Applications of the Law of Sines
Situations involving only the three sides of a triangle, such as determining the area of a triangular plot of land where only the lengths of its sides are known, are unsuitable for the Law of Sines. Similarly, determining the angles in a triangular truss structure where only the lengths of the three sides are known necessitates the use of the Law of Cosines. Finally, scenarios where only two sides and the included angle are known require the Law of Cosines for accurate calculation.

Tim Redaksi