Charles’s Law

Charles’s Law describes the relationship between the volume and temperature of a gas when the pressure is held constant. It’s a fundamental gas law that helps us understand the behavior of gases under specific conditions, particularly useful in various scientific and engineering applications.
Charles’s Law states that the volume of a given amount of gas is directly proportional to its absolute temperature, provided the pressure remains constant. This means that if the temperature increases, the volume will also increase proportionally, and vice versa. This relationship is only valid when the gas behaves ideally, meaning the gas molecules are assumed to have negligible volume and no intermolecular forces.
Mathematical Statement of Charles’s Law
Charles’s Law can be expressed mathematically as:
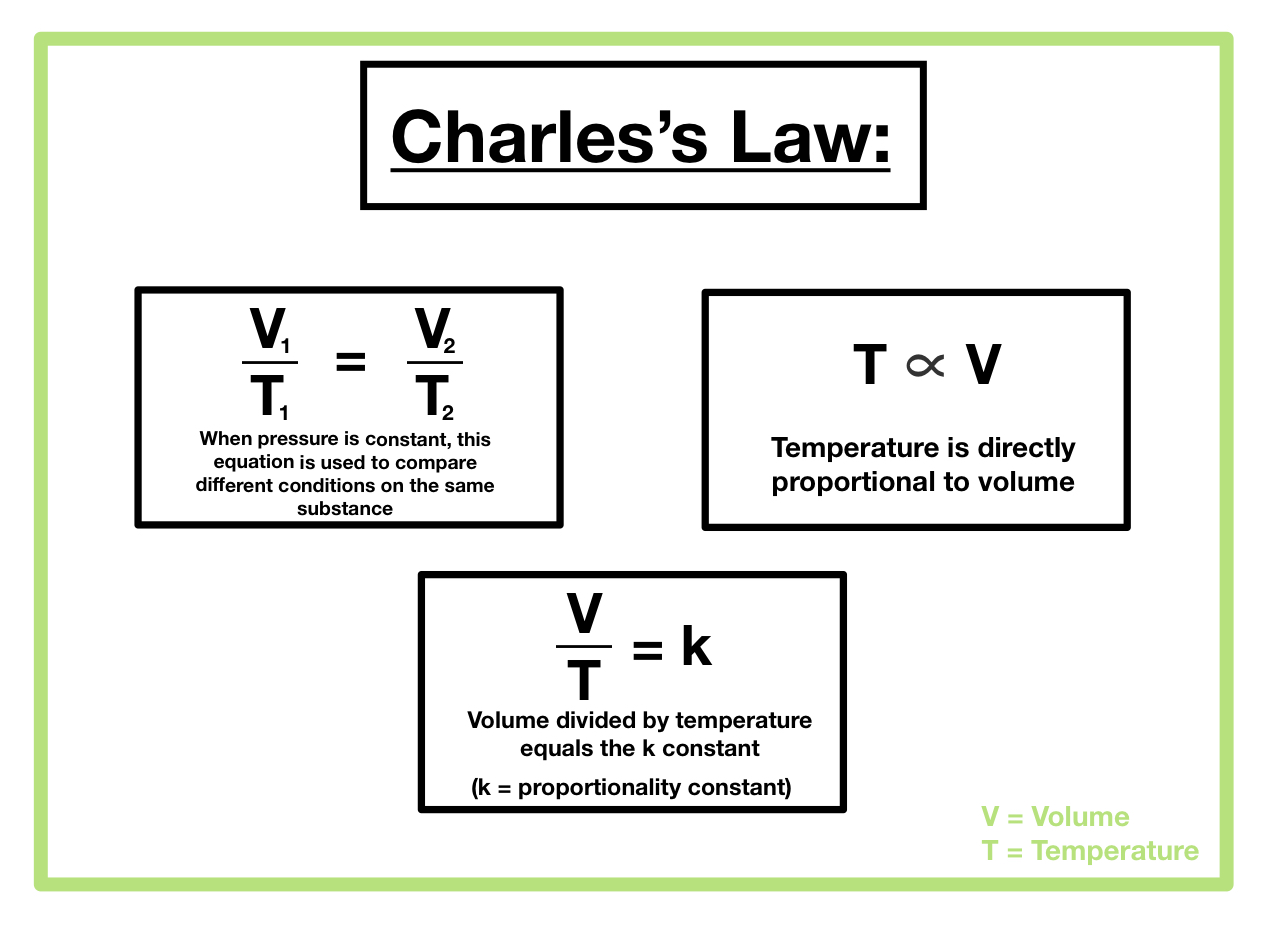
V1/T1 = V2/T2
Where:
* V1 represents the initial volume of the gas.
* T1 represents the initial absolute temperature of the gas (measured in Kelvin).
* V2 represents the final volume of the gas.
* T2 represents the final absolute temperature of the gas (measured in Kelvin).
It is crucial to use the absolute temperature scale (Kelvin) in this equation because Charles’s Law describes a direct proportionality between volume and temperature. Using Celsius or Fahrenheit would introduce a non-zero intercept, distorting the linear relationship. Converting Celsius to Kelvin involves adding 273.15 to the Celsius value.
Assumptions Underlying Charles’s Law
Several assumptions simplify the model and make Charles’s Law applicable. These assumptions, while not perfectly realistic in all situations, allow for a good approximation of gas behavior under many conditions. The primary assumptions are:
The gas is considered to be an ideal gas. This means that the gas molecules are assumed to be point masses with negligible volume and that there are no intermolecular forces of attraction or repulsion between the gas molecules. This simplifies the calculations considerably. Real gases deviate from ideal behavior at high pressures and low temperatures, where intermolecular forces become significant.
The amount of gas (number of moles) remains constant throughout the process. No gas is added or removed from the system during the experiment. This ensures that the observed changes in volume are solely due to changes in temperature.
The pressure of the gas remains constant throughout the process. This is a crucial condition for Charles’s Law to hold true. Any change in pressure would influence the volume independently of temperature, invalidating the direct proportionality.
Relationship between Volume and Temperature
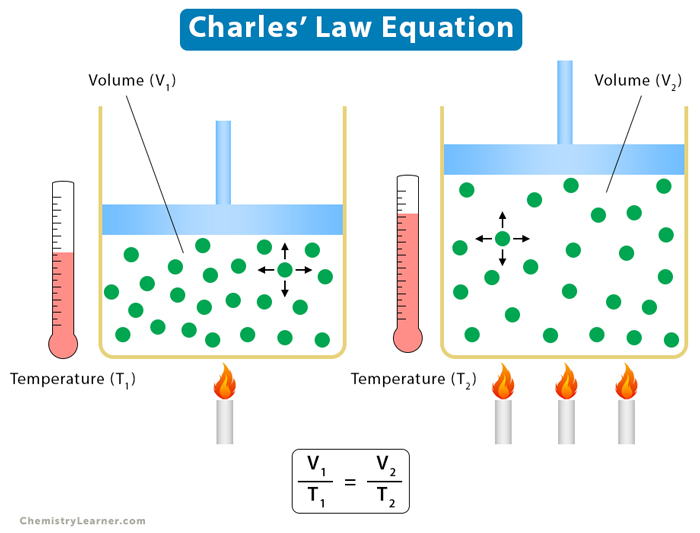
Charles’s Law describes a fundamental relationship between the volume and temperature of a gas when the pressure is held constant. Understanding this relationship is crucial in various scientific and engineering applications, from predicting the behavior of balloons in different atmospheric conditions to designing efficient gas storage systems.
What are the relationships between the variables in charles law – Charles’s Law states that the volume of a gas is directly proportional to its absolute temperature, provided the pressure remains constant. This direct proportionality means that if the absolute temperature of a gas doubles, its volume will also double, and vice versa. This relationship is mathematically represented as V/T = k, where V is the volume, T is the absolute temperature (in Kelvin), and k is a constant.
Volume Changes with Increasing Temperature at Constant Pressure
When the temperature of a gas increases at constant pressure, its volume expands. The gas particles gain kinetic energy, moving faster and colliding more frequently with the container walls. To maintain constant pressure, the volume must increase to accommodate the increased kinetic energy and particle movement. This expansion is directly proportional to the temperature increase. For instance, a balloon filled with air will expand visibly when heated because the air inside expands.
Temperature Changes with Increasing Volume at Constant Pressure
Conversely, if the volume of a gas increases at constant pressure, its temperature must also increase. As the volume expands, the gas particles have more space to move around, resulting in fewer collisions with the container walls per unit time. To maintain the same collision frequency (and thus constant pressure), the average kinetic energy of the particles, and therefore the temperature, must increase. This principle is utilized in processes like adiabatic expansion, where the gas cools down as it expands rapidly without heat exchange with its surroundings.
Sample Data Illustrating the Relationship
| Temperature (K) | Volume (L) |
|---|---|
| 273 | 10 |
| 373 | 13.66 |
| 173 | 6.34 |
| 546 | 20 |
The Importance of Absolute Temperature
Charles’s Law, which describes the direct relationship between the volume and temperature of a gas at constant pressure, relies critically on the use of the absolute temperature scale, specifically Kelvin. Understanding why Kelvin is essential, and the consequences of using other scales, is key to accurately applying and interpreting this fundamental gas law.
The necessity of using absolute temperature stems from the fact that Charles’s Law describes a relationship where the volume of a gas is directly proportional to its absolute temperature. This means that as the absolute temperature increases, the volume increases proportionally, and vice versa. This relationship breaks down if we use relative temperature scales like Celsius or Fahrenheit because these scales have arbitrary zero points. These arbitrary zero points do not represent the absence of thermal energy.
Consequences of Using Non-Absolute Temperature Scales
Using Celsius or Fahrenheit in Charles’s Law calculations leads to inaccurate predictions of gas volume. For instance, if we consider a scenario where the temperature is decreased, using Celsius could incorrectly predict a volume of zero or even a negative volume at 0°C or below. This is physically impossible. The volume of a gas, although it may become extremely small, never actually reaches zero unless the gas is liquefied or solidified. In reality, the gas molecules still possess kinetic energy even at these seemingly low temperatures. Kelvin, on the other hand, avoids this issue by having its zero point at absolute zero, the theoretical temperature at which all molecular motion ceases. This ensures the direct proportionality between volume and temperature holds true across the entire range of temperatures.
Comparison of Temperature Scale Effects on Gas Volume
Let’s consider a simple example: a gas with an initial volume of 10 liters at 273 K (0°C). If we double the absolute temperature to 546 K (273°C), Charles’s Law predicts the volume will also double to 20 liters. However, if we were to use the Celsius scale and simply double the temperature from 0°C to 0°C, the calculation would incorrectly suggest no change in volume. Similarly, if we tried to extrapolate to lower temperatures using the Celsius scale, we’d arrive at nonsensical results. This illustrates how the choice of temperature scale significantly impacts the accuracy and physical meaningfulness of Charles’s Law calculations. The consistent, direct proportionality only holds true when using the absolute Kelvin scale.
Limitations of Charles’s Law: What Are The Relationships Between The Variables In Charles Law
Charles’s Law, while a valuable simplification of gas behavior, doesn’t perfectly describe the relationship between volume and temperature under all conditions. Real gases deviate from the ideal behavior predicted by the law, particularly at high pressures and low temperatures. This deviation arises because Charles’s Law is based on the ideal gas model, which makes several simplifying assumptions about gas molecules.
The accuracy of Charles’s Law predictions diminishes as conditions move away from those assumed in the ideal gas model. Specifically, the law assumes that gas molecules have negligible volume and exert no intermolecular forces on each other. These assumptions are reasonably accurate at low pressures and high temperatures, where the molecules are far apart and their kinetic energy is high enough to overcome weak intermolecular attractions. However, at high pressures and low temperatures, these assumptions break down, leading to observable discrepancies between experimental results and Charles’s Law predictions.
High Pressure Effects, What are the relationships between the variables in charles law
At high pressures, the volume occupied by the gas molecules themselves becomes significant compared to the total volume of the container. The ideal gas law neglects the volume of the gas molecules, but in reality, this volume reduces the space available for the gas to expand, leading to a smaller observed volume increase with temperature than predicted by Charles’s Law. For instance, consider a gas compressed into a small container. As the temperature increases, the increased kinetic energy of the molecules causes more frequent collisions with the container walls. However, the finite size of the molecules means that they cannot move entirely freely, limiting the overall volume expansion. This effect is more pronounced at higher pressures where the molecules are closer together.
Low Temperature Effects
At low temperatures, the kinetic energy of gas molecules decreases significantly. Intermolecular forces, which are normally negligible at higher temperatures, become more prominent. These attractive forces cause the molecules to clump together, reducing the effective number of independent particles contributing to the pressure and volume. This results in a smaller volume increase with temperature than predicted by Charles’s Law. For example, consider a gas approaching its liquefaction point. As the temperature drops, intermolecular attractive forces become stronger, causing the gas to deviate significantly from ideal behavior. The molecules are no longer free to move independently, and the volume change with temperature is not accurately described by the simple proportionality of Charles’s Law.

Tim Redaksi