Variables in Charles’s Law

Charles’s Law describes a fundamental relationship between the volume and temperature of a gas. Understanding the variables involved is crucial to applying this law accurately in various scientific and engineering contexts. This section will detail the key variables and the conditions under which Charles’s Law holds true.
What is the relationship between te variables in charles law – The two primary variables in Charles’s Law are the volume (V) and the absolute temperature (T) of a gas. It’s crucial to note that temperature must be expressed in Kelvin (K), not Celsius or Fahrenheit, as absolute temperature scales provide a true zero point, reflecting the absence of thermal energy.
The Relationship Between Volume and Temperature, What is the relationship between te variables in charles law
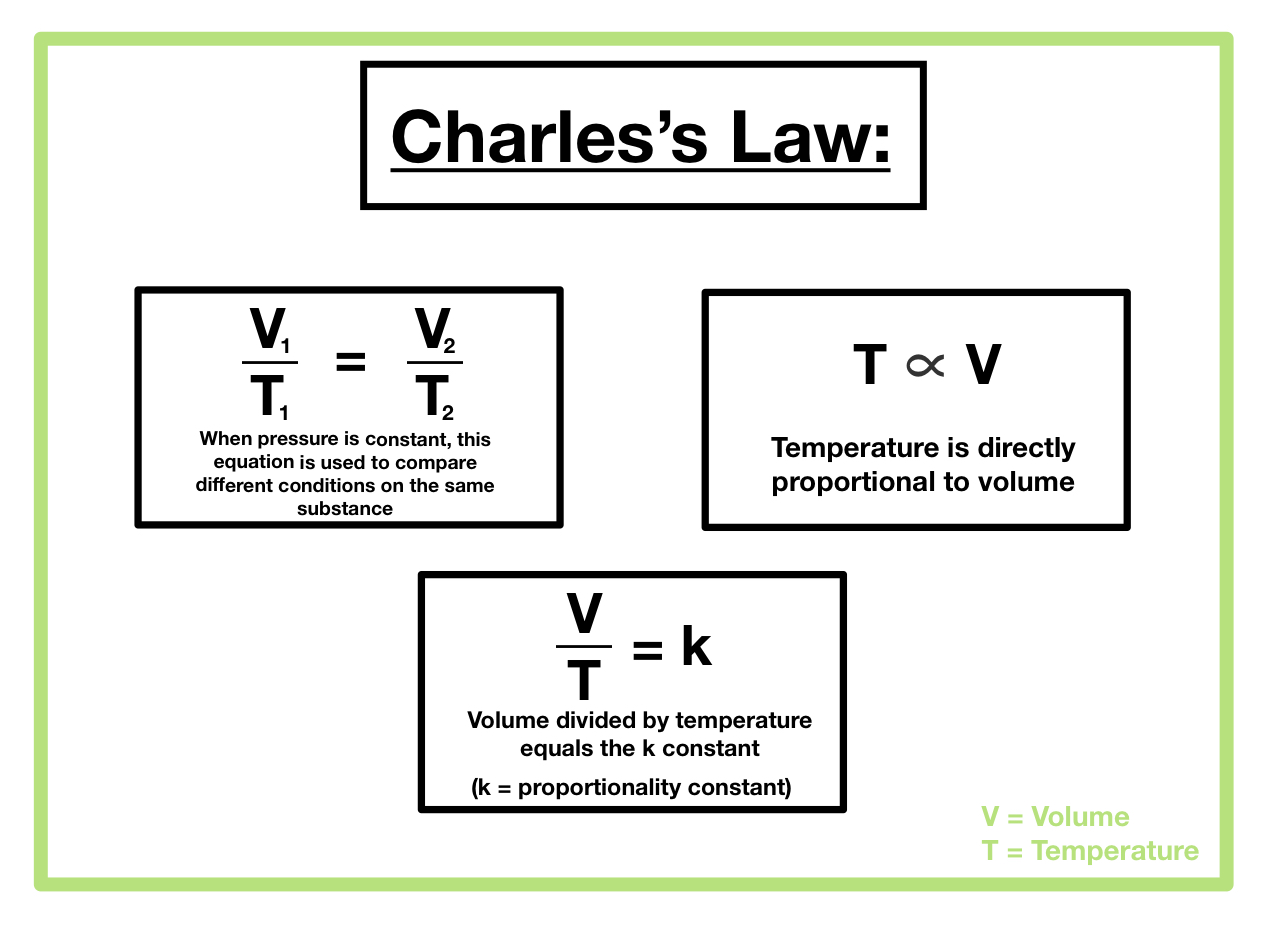
Charles’s Law states that at constant pressure and amount of gas, the volume of a gas is directly proportional to its absolute temperature. This means that if the temperature of a gas increases, its volume will also increase proportionally, and vice-versa. Mathematically, this relationship is expressed as:
V ∝ T or V/T = k
where ‘k’ is a constant value that depends on the pressure and the amount of gas. This equation implies that the ratio of volume to absolute temperature remains constant under the specified conditions. For example, if the temperature of a gas doubles, its volume will also double, assuming pressure and amount of gas remain unchanged. Conversely, halving the temperature will halve the volume.
Conditions for Charles’s Law Applicability
Charles’s Law is only applicable under specific conditions: the pressure and the amount of gas (number of moles) must remain constant. If either of these factors changes, the relationship between volume and temperature will deviate from the simple proportionality described by Charles’s Law. Consider, for example, a balloon filled with air. If we heat the balloon, its volume increases (Charles’s Law). However, if we also allow air to escape (changing the amount of gas), the volume increase will be less than predicted by Charles’s Law alone. Similarly, if the external pressure changes significantly (for instance, by taking the balloon to a higher altitude), the volume will not follow the direct proportionality with temperature as precisely. Therefore, maintaining constant pressure and amount of gas is paramount for the accurate application of Charles’s Law.
Graphical Representation of Charles’s Law

Charles’s Law, which describes the direct relationship between the volume and temperature of a gas at constant pressure, is best understood visually. A graph provides a clear and concise way to represent this relationship, allowing for easy interpretation and prediction of gas behavior under varying conditions.
A graph illustrating Charles’s Law plots volume (V) on the y-axis and absolute temperature (T) on the x-axis. Since the relationship is directly proportional (meaning that as temperature increases, volume increases proportionally), the resulting graph will be a straight line passing through the origin (0,0). This is because at absolute zero (0 Kelvin), the volume of an ideal gas would theoretically be zero. Real-world gases, however, do not behave ideally at very low temperatures.
Sample Data and Graph Description
The following table provides sample data points that could be used to create a graph illustrating Charles’s Law. These values represent a hypothetical gas kept at a constant pressure. Remember that the temperature must be expressed in Kelvin (K).
| Temperature (K) | Volume (L) |
|---|---|
| 100 | 1.0 |
| 200 | 2.0 |
| 300 | 3.0 |
| 400 | 4.0 |
The graph generated from this data would show a straight line with a positive slope. The slope of the line represents the constant of proportionality between volume and temperature at constant pressure. A steeper slope indicates a larger change in volume for a given change in temperature. The y-intercept is zero, representing the theoretical point where volume is zero at absolute zero temperature. The straight line nature of the graph visually confirms the direct proportionality between volume and absolute temperature described by Charles’s Law. Deviations from this straight line in experimental data might indicate that the pressure was not truly constant, or that the gas is not behaving ideally. For instance, if the gas were to undergo a phase change (like condensation), the relationship would no longer be linear.
Illustrative Examples of Charles’s Law: What Is The Relationship Between Te Variables In Charles Law
Charles’s Law, stating that the volume of a gas is directly proportional to its absolute temperature at constant pressure, is readily observable in everyday phenomena. Understanding its application helps explain various processes involving gases. Let’s explore some illustrative examples.
Hot Air Balloon Inflation
A hot air balloon provides a classic demonstration of Charles’s Law. The balloon’s envelope is filled with air, which is then heated using a burner. As the air within the balloon is heated, its temperature increases. According to Charles’s Law, this temperature increase causes a corresponding increase in the volume of the air. The expanded air becomes less dense than the surrounding cooler air, creating buoyant force that lifts the balloon. The burner continuously heats the air, maintaining the elevated temperature and thus the increased volume, allowing the balloon to remain aloft. Conversely, as the burner is turned off, the air cools, its volume decreases, and the balloon descends. The relationship between the volume and temperature remains directly proportional throughout the flight, assuming atmospheric pressure remains relatively constant.
Sealed Container Pressure Changes
Consider a sealed rigid container filled with a gas at a specific temperature and pressure. If we increase the temperature of the container, the gas molecules within gain kinetic energy, moving faster and colliding more frequently and forcefully with the container walls. However, because the container is sealed and rigid, its volume remains constant. This increased kinetic energy and the resulting more frequent and forceful collisions manifest as an increase in pressure within the container. Conversely, if the temperature of the container is decreased, the gas molecules slow down, their collisions become less frequent and forceful, resulting in a decrease in pressure. This demonstrates that while volume is held constant, pressure and temperature are directly related within a sealed system. The relationship isn’t directly proportional as Charles’ Law states (because volume is constant, not pressure), but the principle of temperature affecting the gas’s behavior is clearly shown.
Weather Balloon Volume Changes
Weather balloons are launched into the atmosphere to collect meteorological data. As the balloon ascends, it encounters progressively lower atmospheric pressures and temperatures. The decrease in atmospheric pressure allows the gas inside the balloon to expand. Simultaneously, the decrease in temperature would cause the gas volume to contract. The net effect on the balloon’s volume depends on the relative magnitudes of these opposing effects. At higher altitudes, the decrease in temperature usually dominates, resulting in a smaller overall balloon volume than at lower altitudes. However, if the pressure drop is significant enough, the expansion due to reduced pressure could outweigh the contraction from temperature drop, leading to a larger volume at higher altitudes than initially expected. Precise predictions require considering both temperature and pressure changes at various altitudes. For instance, a balloon launched on a particularly cold day might experience a smaller volume increase at higher altitudes compared to a balloon launched on a warmer day, even at the same pressure differences.

Tim Redaksi