Understanding Coulomb’s Law: How To Add Forces Using Coulomb’s Law

Coulomb’s Law is a fundamental principle in physics that describes the electrostatic interaction between electrically charged particles. It quantifies the force of attraction or repulsion between these particles, laying the groundwork for understanding a wide range of phenomena from the behavior of atoms to the workings of electronic devices.
Coulomb’s Law: Formula and Variables
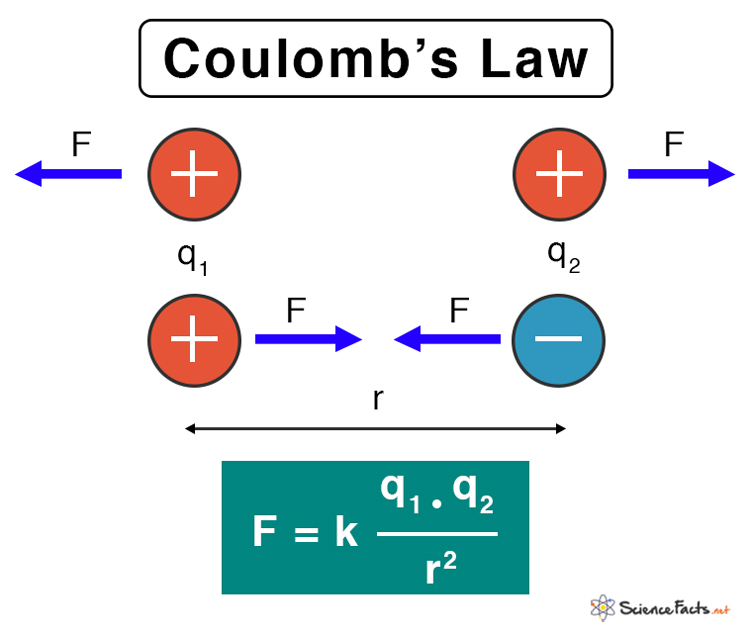
Coulomb’s Law states that the force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. This relationship is mathematically expressed as:
F = ke * |q1q2| / r2
Where:
* F represents the electrostatic force (in Newtons). This force is a vector quantity, meaning it has both magnitude and direction.
* ke is Coulomb’s constant, a proportionality constant that depends on the medium in which the charges are situated. In a vacuum, its value is approximately 8.98755 × 109 N⋅m2/C2.
* q1 and q2 represent the magnitudes of the two point charges (in Coulombs).
* r represents the distance between the centers of the two charges (in meters). The square of this distance indicates the rapid decrease in force with increasing separation. The absolute value signs around q1q2 ensure that the force is always positive, regardless of whether the charges are positive or negative. The direction of the force is determined separately, based on the signs of the charges.
Applications of Coulomb’s Law
Coulomb’s Law finds application in numerous areas of science and engineering. For instance, it’s crucial in understanding the structure of atoms and molecules, where the electrostatic forces between protons and electrons determine the stability and properties of matter. In chemistry, it helps explain ionic bonding, where oppositely charged ions attract each other to form stable compounds. In the field of electronics, Coulomb’s Law is fundamental to the design and operation of electronic devices, such as capacitors and transistors. Even in meteorology, understanding the electrostatic interactions between charged particles in the atmosphere is essential for predicting lightning strikes.
Significance of Coulomb’s Constant
Coulomb’s constant (ke) is a fundamental physical constant that reflects the strength of the electrostatic interaction in a given medium. Its value in a vacuum is a precisely determined constant, reflecting the permittivity of free space (ε0) through the relationship: ke = 1/(4πε0). The constant’s magnitude signifies the relative strength of the electrostatic force compared to other fundamental forces in nature. A larger value would imply a stronger electrostatic force, significantly altering the behavior of charged particles and the systems they constitute. The value of ke is also affected by the dielectric constant of the medium; in materials other than a vacuum, the force is reduced by a factor equal to the dielectric constant of the material.
Attractive and Repulsive Forces
The following table summarizes the nature of the electrostatic force depending on the charges involved:
| Charge of q1 | Charge of q2 | Nature of Force | Force Direction |
|---|---|---|---|
| Positive | Positive | Repulsive | Away from each other |
| Negative | Negative | Repulsive | Away from each other |
| Positive | Negative | Attractive | Towards each other |
| Negative | Positive | Attractive | Towards each other |
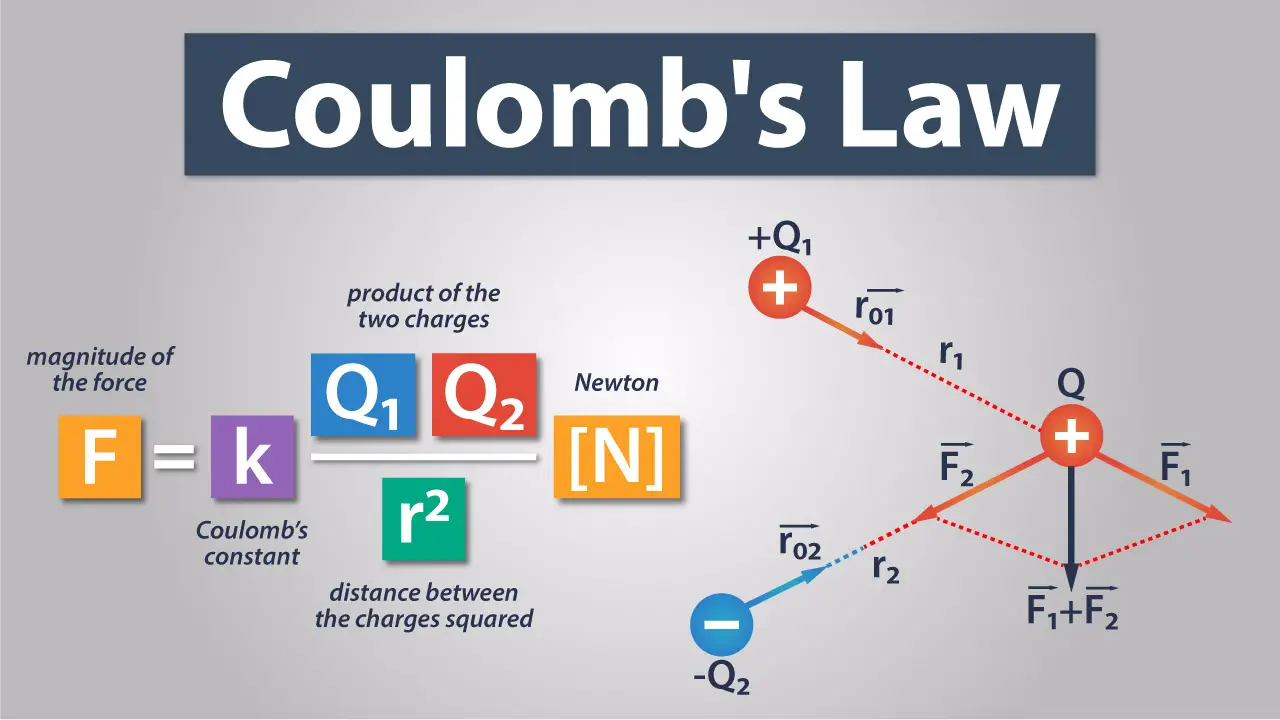
Adding Forces from Multiple Charges
When dealing with more than two charges, calculating the net force on a single charge requires a vector summation of the individual forces exerted by each of the other charges. This involves applying Coulomb’s Law individually to each pair of interacting charges and then combining the resulting force vectors. The principle of superposition is crucial here: the total force on a charge is the vector sum of the forces due to each other charge acting independently.
Calculating Net Force on a Single Charge
To determine the net force on a specific charge due to multiple other charges, we must first calculate the force exerted by each individual charge on the target charge using Coulomb’s Law:
F = k * |q1 * q2| / r²
where F is the force, k is Coulomb’s constant (8.98755 × 10⁹ N⋅m²/C²), q1 and q2 are the magnitudes of the charges, and r is the distance between them. Remember that force is a vector quantity; therefore, direction must be considered. After calculating each individual force, we resolve these forces into their x and y components. Finally, we sum the x-components and y-components separately to find the net force’s x and y components. The magnitude and direction of the net force are then calculated using the Pythagorean theorem and trigonometry.
Example: Charges Arranged in a Line
Consider three charges, q1 = +2 µC, q2 = -4 µC, and q3 = +3 µC, arranged along a straight line. q1 is at x = 0 cm, q2 is at x = 5 cm, and q3 is at x = 10 cm. Let’s calculate the net force on q2.
First, calculate the force exerted by q1 on q2 (F12): The distance r12 is 5 cm (0.05 m). The force is attractive (opposite charges), and directed towards q1 (negative x-direction).
F12 = k * |q1 * q2| / r12² = (8.98755 × 10⁹ N⋅m²/C²) * (2 × 10⁻⁶ C) * (4 × 10⁻⁶ C) / (0.05 m)² ≈ -28.76 N
Next, calculate the force exerted by q3 on q2 (F32): The distance r32 is 5 cm (0.05 m). The force is repulsive (like charges), and directed towards the positive x-direction.
F32 = k * |q2 * q3| / r32² = (8.98755 × 10⁹ N⋅m²/C²) * (4 × 10⁻⁶ C) * (3 × 10⁻⁶ C) / (0.05 m)² ≈ 43.14 N
The net force on q2 is the sum of F12 and F32: Fnet = F12 + F32 = -28.76 N + 43.14 N = 14.38 N. The net force on q2 is 14.38 N in the positive x-direction.
Example: Charges Arranged in a Triangle
Let’s consider three charges arranged at the vertices of a right-angled triangle. q1 = +2 µC is at (0, 0), q2 = -4 µC is at (3 cm, 0), and q3 = +3 µC is at (0, 4 cm). We’ll calculate the net force on q1.
First, calculate the force exerted by q2 on q1 (F21): The distance r21 is 3 cm (0.03 m). This force is attractive and acts along the negative x-axis.
F21 = k * |q1 * q2| / r21² ≈ -79.89 N (along the negative x-axis)
Next, calculate the force exerted by q3 on q1 (F31): The distance r31 is 4 cm (0.04 m). This force is repulsive and acts along the positive y-axis.
F31 = k * |q1 * q3| / r31² ≈ 33.71 N (along the positive y-axis)
To find the net force, we use vector addition. The net force on q1 has components Fx = -79.89 N and Fy = 33.71 N. The magnitude of the net force is:
|Fnet| = √(Fx² + Fy²) ≈ 86.26 N
The direction (θ) of the net force is given by:
θ = tan⁻¹(Fy / Fx) ≈ 157.6° (measured counterclockwise from the positive x-axis)
Advanced Applications
Coulomb’s Law, while seemingly simple, forms the bedrock of understanding electrostatic interactions. However, its application extends beyond simple point charges to more complex scenarios, revealing both its power and its limitations. This section explores these advanced applications and nuances.
Continuous Charge Distributions
Dealing with objects possessing a continuous distribution of charge, like a uniformly charged rod or sphere, requires a slightly different approach. We can’t simply treat them as point charges. Instead, we divide the object into infinitesimal charge elements, dq, and apply Coulomb’s Law to each element. The total force is then found by integrating the contributions from all these elements. This integration process often involves calculus, requiring knowledge of vector addition and integration techniques. For example, calculating the electric field at a point due to a uniformly charged rod involves integrating the contributions from each small segment of the rod, considering both the distance and the direction of the force from each segment. The result is a more complex mathematical expression compared to the simple point-charge scenario, but it allows us to accurately predict the electric field or force from extended objects.
Limitations of Coulomb’s Law
Coulomb’s Law is a remarkably accurate description of electrostatic interactions under specific conditions. However, it breaks down in certain situations. Firstly, it’s only valid for static charges; it doesn’t accurately describe the forces between moving charges at speeds approaching the speed of light. In such cases, relativistic effects become significant, requiring a more sophisticated framework such as electromagnetism as described by Maxwell’s equations. Secondly, Coulomb’s Law is only an approximation when dealing with macroscopic objects. The law assumes point charges, which means the dimensions of the charged objects are negligible compared to the distance separating them. When the dimensions are comparable, or even larger than the distance between them, the law becomes less accurate. Finally, Coulomb’s Law doesn’t account for the effects of polarization, which describes the redistribution of charge within a material due to an external electric field. This is particularly relevant when dealing with dielectric materials.
Comparison with Newton’s Law of Universal Gravitation, How to add forces using coulomb’s law
Coulomb’s Law and Newton’s Law of Universal Gravitation share a striking similarity in their mathematical form. Both describe inverse-square laws, meaning the force is inversely proportional to the square of the distance between the interacting objects.
Fc = ke * |q1q2| / r2
and
Fg = G * m1m2 / r2
. However, there are crucial differences. Coulomb’s Law describes the force between electric charges, which can be either attractive or repulsive, while Newton’s Law describes the force between masses, which is always attractive. The strength of the forces also differs dramatically; the electrostatic force is significantly stronger than the gravitational force. This explains why gravitational effects are generally negligible at the atomic or molecular level, where electrostatic forces dominate.
Validity of the Point Charge Approximation
The point charge approximation simplifies calculations significantly. It’s valid when the size of the charged objects is much smaller than the distance separating them. For instance, calculating the force between two charged spheres separated by a distance many times larger than their diameters can be accurately approximated using the point charge model. However, if the spheres are close together, or if their size is comparable to the separation distance, this approximation breaks down. In such cases, the continuous charge distribution approach described earlier becomes necessary for accurate results. A good rule of thumb is that the point charge approximation is reasonably accurate if the distance between the centers of the charges is at least ten times greater than the largest dimension of the charged objects.

Tim Redaksi