Illustrative Examples

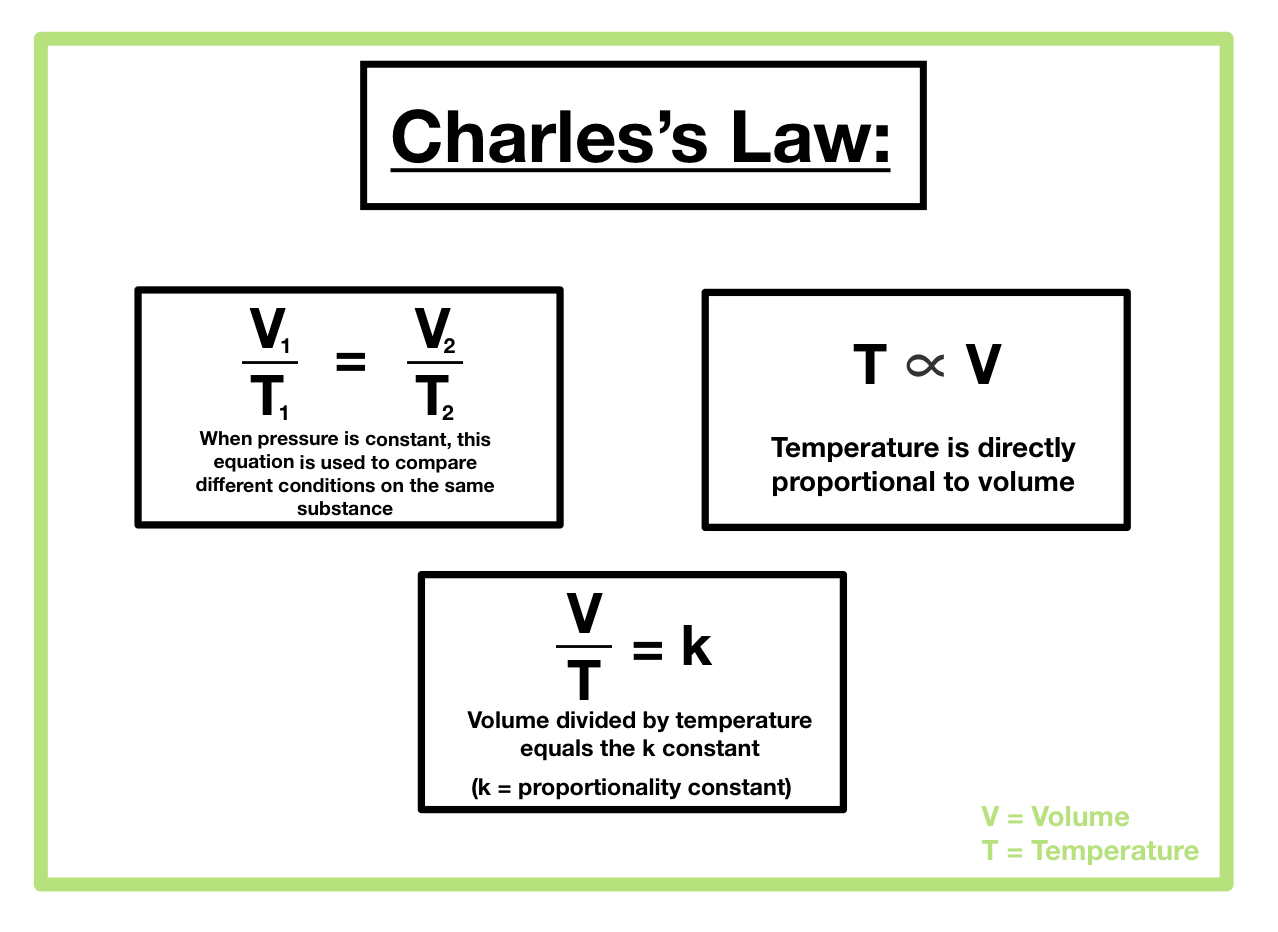
Let’s explore Charles’s Law with some practical examples. Understanding how volume and temperature relate under constant pressure and gas amount is crucial for many applications in chemistry and physics. The following examples demonstrate the direct proportionality between these two variables.
Illustrative Examples of Charles’s Law
The table below presents three scenarios illustrating the relationship between the initial and final volumes and temperatures of a gas, assuming constant pressure and amount of gas. Remember that temperature must be expressed in Kelvin (K) for Charles’s Law calculations.
| Initial Volume (L) | Initial Temperature (K) | Final Volume (L) | Final Temperature (K) |
|---|---|---|---|
| 2.0 | 273 | 4.0 | 546 |
| 5.0 | 300 | 2.5 | 150 |
| 1.0 | 200 | 1.5 | 300 |
Graphical Representation of Charles’s Law
A graph illustrating Charles’s Law would clearly depict the direct proportionality between volume and temperature. The x-axis would represent temperature (in Kelvin), and the y-axis would represent volume (in liters). The graph would show a straight line passing through the origin (0,0). This indicates that as the temperature increases, the volume increases proportionally, and vice-versa, provided the pressure and amount of gas remain constant. The line’s slope represents the constant of proportionality, which depends on the amount of gas and the pressure. A steeper slope would indicate a larger volume change for a given temperature change. The positive slope confirms the direct relationship between volume and temperature as predicted by Charles’s Law. The line will not extend into negative temperature or volume values, as these are physically impossible.
Applications of Charles’s Law: What Is The Constant Variable Of The Charles Law
Charles’s Law, describing the direct relationship between the volume and temperature of a gas at constant pressure, has far-reaching implications in various scientific and engineering fields. Its principles underpin numerous practical applications, allowing us to predict and explain a wide range of phenomena involving gases.
Understanding Charles’s Law is crucial for accurately predicting gas behavior under changing temperature conditions. This understanding is vital in diverse fields, from weather forecasting to the design of aircraft and industrial processes.
Meteorological Applications
The relationship between temperature and air volume is fundamental to understanding weather patterns. As air warms, it expands, becoming less dense and rising. Conversely, cooling air contracts, becoming denser and sinking. This process drives convection currents, influencing wind patterns, cloud formation, and ultimately, weather systems. For example, the formation of thermals (rising columns of warm air) used by birds and gliders relies directly on the principles of Charles’s Law. The expansion of air masses due to heating contributes significantly to the development of high- and low-pressure systems, influencing weather forecasts and predictions.
Aviation Applications
Charles’s Law plays a critical role in aviation safety and efficiency. The volume of gases, including the air within aircraft tires and fuel tanks, changes significantly with altitude and temperature fluctuations. Aircraft designers must account for these variations to ensure safe operation. For instance, aircraft tires need to be properly inflated at ground level to account for the expansion that occurs at higher altitudes where temperatures are significantly lower. Similarly, the expansion and contraction of fuel in aircraft tanks must be considered during flight planning and fuel calculations to prevent potential issues.
Engineering Applications
Engineers utilize Charles’s Law in various applications, particularly those involving gas storage and transportation. The design of gas storage tanks and pipelines must consider the expansion and contraction of gases due to temperature changes. This is crucial for preventing over-pressurization or leaks, ensuring safe and efficient operation. Furthermore, the principle is applied in the design of hot air balloons, where the controlled heating and cooling of air within the balloon envelope directly controls its buoyancy and altitude. The expansion of the heated air reduces its density, causing the balloon to rise.
Limitations of Charles’s Law

Charles’s Law, while a valuable tool for understanding gas behavior, is not universally applicable. Its accuracy depends heavily on the assumption that the gas being studied behaves ideally. Real-world gases often deviate from this ideal behavior, leading to inaccuracies in predictions made using Charles’s Law. These deviations become particularly significant under specific conditions of temperature and pressure.
The limitations stem primarily from the inherent assumptions made in deriving Charles’s Law. It assumes that gas molecules occupy negligible volume and that there are no intermolecular forces between them. These assumptions are reasonably accurate for many gases at moderate temperatures and pressures, but break down under extreme conditions.
Deviations from Ideal Gas Behavior at Low Temperatures and High Pressures
At very low temperatures, the kinetic energy of gas molecules decreases significantly. This reduction in energy means that intermolecular attractive forces, which are always present to some degree, become more influential. These forces cause the gas molecules to clump together more, reducing the volume occupied by the gas compared to what would be predicted by Charles’s Law. Similarly, at high pressures, the volume occupied by the gas molecules themselves becomes a non-negligible fraction of the total volume. The assumption that the gas molecules occupy negligible volume is no longer valid, resulting in deviations from the law. For instance, consider trying to apply Charles’s Law to predict the volume of a gas close to its liquefaction point. The strong intermolecular forces would lead to significant underestimation of the actual volume. Conversely, at extremely high pressures, the volume of the gas molecules themselves would significantly affect the final volume, again leading to inaccuracy.
The Ideal Gas Concept and its Relevance, What is the constant variable of the charles law
The concept of an “ideal gas” is a theoretical construct that simplifies the behavior of real gases. An ideal gas is defined as a gas that perfectly obeys the ideal gas law (PV = nRT), implying that there are no intermolecular forces and that the volume of the gas molecules is negligible. Charles’s Law, being a direct consequence of the ideal gas law, relies on these same assumptions. Therefore, the closer a real gas behaves like an ideal gas, the more accurately Charles’s Law will predict its behavior. Noble gases, such as helium and argon, exhibit behavior closer to that of an ideal gas under a wider range of conditions compared to gases like carbon dioxide or water vapor, which have stronger intermolecular forces. The degree of deviation from ideal gas behavior can be quantified using the compressibility factor (Z), where Z = PV/nRT. For an ideal gas, Z = 1. Deviations from Z=1 indicate non-ideal behavior.

Tim Redaksi