Identifying the Variables in Boyle’s Law
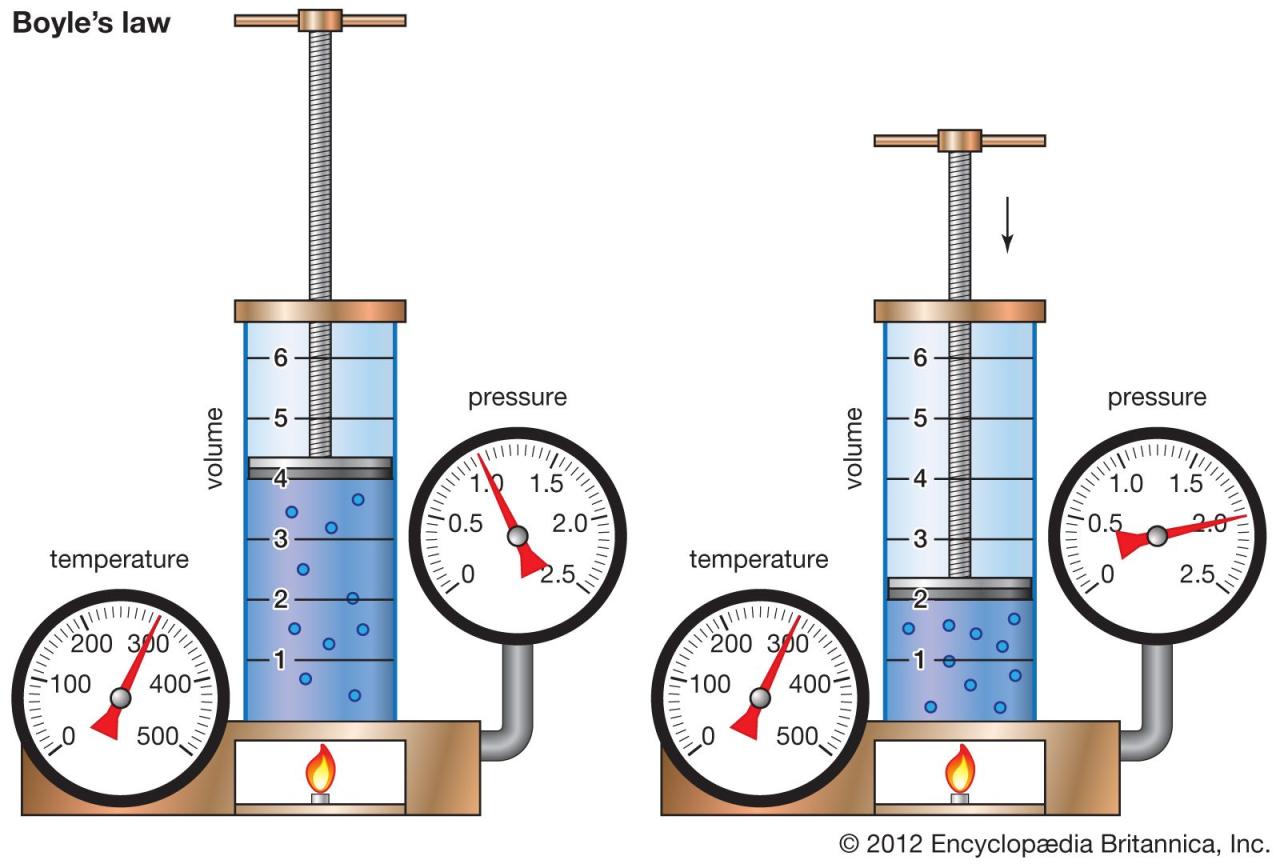
Boyle’s Law describes the inverse relationship between the pressure and volume of a gas when the temperature and the amount of gas are held constant. Understanding the variables involved is crucial for applying this law accurately in various scientific and engineering contexts. This section will detail these variables and the units commonly used to measure them.
What are the variables in boyles laws – Boyle’s Law involves three key variables: pressure (P), volume (V), and the amount of gas (n), measured in moles. While temperature (T) also affects gas behavior, Boyle’s Law specifically focuses on the relationship between pressure and volume under isothermal conditions (constant temperature). The amount of gas (n) remains constant throughout the experiment for Boyle’s Law to hold true. Changes in any of these variables will affect the others according to the law’s inverse proportionality.
Units of Measurement for Boyle’s Law Variables
Accurate application of Boyle’s Law requires consistent use of units. The choice of units depends on the context of the problem and the available measuring instruments. The International System of Units (SI) provides a standardized system, but other units are frequently encountered.
| Variable | SI Unit | Common Alternatives | Description |
|---|---|---|---|
| Pressure (P) | Pascal (Pa) | Atmosphere (atm), millimeters of mercury (mmHg), torr, pounds per square inch (psi) | Force exerted per unit area. |
| Volume (V) | Cubic meter (m3) | Liter (L), milliliter (mL), cubic centimeter (cm3) | Amount of three-dimensional space occupied by the gas. |
| Amount of Gas (n) | Mole (mol) | — | Number of gas particles (atoms or molecules). One mole contains Avogadro’s number (approximately 6.022 x 1023) of particles. |
The Importance of Constant Variables: What Are The Variables In Boyles Laws

Boyle’s Law, which describes the inverse relationship between the pressure and volume of a gas, is fundamentally reliant on maintaining certain conditions as constants. Understanding the crucial role of these constant variables is key to accurately applying and interpreting the law. Failure to control these variables leads to inaccurate results and a skewed understanding of the pressure-volume relationship.
The accuracy of Boyle’s Law hinges on keeping both the temperature and the amount of gas (number of moles) constant throughout the experiment. If either of these variables changes, the observed pressure-volume relationship will deviate from the expected inverse proportionality. This deviation occurs because changes in temperature and the amount of gas directly influence the kinetic energy and the number of gas particles, respectively, both of which significantly affect pressure and volume.
The Impact of Non-Constant Temperature
If the temperature of the gas is not held constant during a Boyle’s Law experiment, the observed relationship between pressure and volume will not follow the inverse proportionality described by the law. Increasing the temperature increases the kinetic energy of the gas molecules, causing them to collide more frequently and with greater force against the container walls. This leads to an increase in pressure, even if the volume remains the same. Conversely, decreasing the temperature reduces the kinetic energy, resulting in lower pressure. This means that a simple compression of the gas at a higher temperature will yield a higher final pressure than the same compression at a lower temperature, obscuring the pure Boyle’s Law relationship. Therefore, precise temperature control is paramount for accurate experimental results.
A Thought Experiment: Temperature Variation’s Effect, What are the variables in boyles laws
Imagine two identical rigid containers, each filled with the same amount of an ideal gas. Container A is kept at a constant temperature of 25°C, while Container B is heated to 100°C. Both containers are then subjected to the same volume reduction. According to Boyle’s Law, the pressure increase in Container A should be directly proportional to the volume decrease. However, Container B will show a significantly greater pressure increase than Container A because the increased temperature elevates the kinetic energy of the gas molecules, leading to more forceful collisions and higher pressure. This demonstrates how temperature variations introduce significant error when attempting to verify Boyle’s Law. The relationship between pressure and volume in Container B will not accurately reflect the inverse proportionality described by Boyle’s Law.

Tim Redaksi