Identifying Constants in Boyle’s Law Experiments: What Remain Constant In Boyle’s Law

Boyle’s Law, which describes the inverse relationship between the pressure and volume of a gas at constant temperature, relies on careful control of experimental variables. Understanding which factors remain constant and how they influence the results is crucial for accurate interpretation and application of the law. This section will delve into the identification of these constants within the context of a typical Boyle’s Law experiment.
The variables involved in Boyle’s Law experiments are pressure (P) and volume (V) of a gas. These are the variables that are directly measured and observed to change in relation to each other. The relationship between these two variables is the focus of the experiment and forms the core of Boyle’s Law.
Controlled Variables in Boyle’s Law Experiments
Maintaining consistent conditions beyond the pressure and volume is essential for a valid Boyle’s Law experiment. These controlled variables ensure that any observed changes in pressure and volume are solely due to their inverse relationship, and not influenced by other factors. This control allows for a clean demonstration of the law.
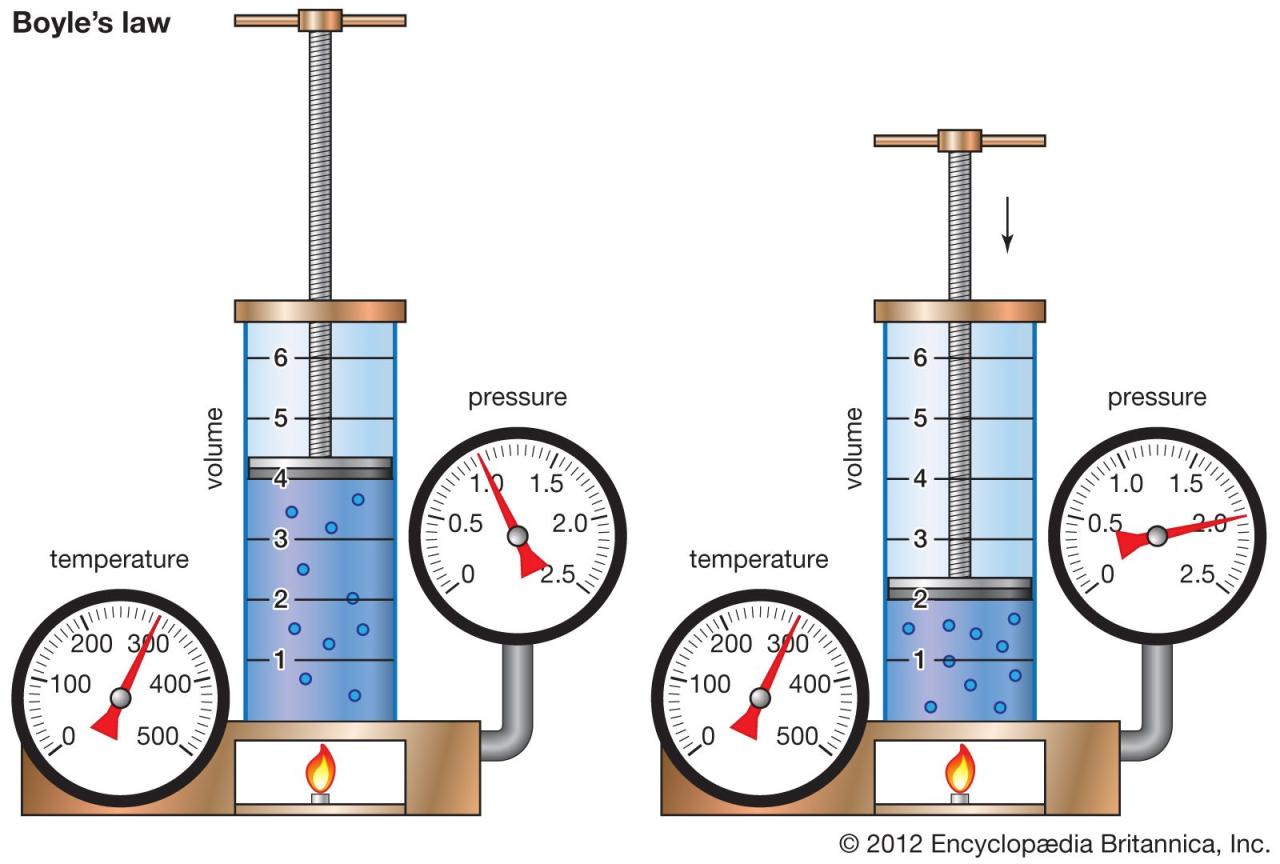
Examples of controlled variables in typical Boyle’s Law experiments include the amount of gas (number of moles, n), and most importantly, the temperature (T). Keeping the amount of gas constant prevents changes in pressure and volume due to adding or removing gas molecules. Precise temperature control ensures that the gas’s kinetic energy, and thus its pressure and volume behavior, remain consistent throughout the experiment. For example, a common experimental setup might involve a trapped sample of air within a syringe, where the volume is adjusted and the corresponding pressure change is measured. In this case, the amount of air and the temperature of the surrounding environment would be carefully controlled.
The Importance of Maintaining Constant Temperature in Boyle’s Law Experiments
Maintaining a constant temperature is paramount in Boyle’s Law experiments. Temperature directly affects the kinetic energy of gas molecules. Increased temperature leads to faster-moving molecules, resulting in increased collisions with the container walls and therefore higher pressure for a given volume. Conversely, lower temperatures lead to slower-moving molecules and reduced pressure. If the temperature fluctuates during the experiment, the observed pressure-volume relationship will deviate from the ideal inverse relationship predicted by Boyle’s Law, leading to inaccurate results. This deviation is because the observed changes will be a combination of the inverse pressure-volume relationship and the effect of temperature changes. Therefore, accurate temperature control ensures that the measured pressure and volume changes accurately reflect Boyle’s Law.
Impact of Non-Constant Temperature on Experimental Results
If the temperature is not kept constant during a Boyle’s Law experiment, the experimental results will not accurately reflect the inverse relationship between pressure and volume. For instance, if the temperature increases during the experiment, the pressure will appear higher than expected for a given volume, giving a false impression of a less pronounced inverse relationship. Similarly, a decrease in temperature would lead to an underestimation of the pressure and an apparent weakening of the inverse relationship. These deviations can be significant, rendering the experimental data unreliable and unsuitable for verifying or illustrating Boyle’s Law. In essence, a variable temperature introduces an additional, uncontrolled variable that confounds the relationship between pressure and volume, masking the true nature of Boyle’s Law.
The Amount of Gas
Boyle’s Law, a fundamental gas law, describes the inverse relationship between the pressure and volume of a gas at a constant temperature. Understanding the conditions under which this law holds true is crucial for its accurate application. A key factor often overlooked is the necessity of maintaining a constant amount of gas.
The amount of gas, typically expressed in moles (a unit representing the number of particles), must remain unchanged throughout an experiment designed to demonstrate Boyle’s Law. If the number of moles of gas changes, the pressure-volume relationship will deviate from the inverse proportionality described by Boyle’s Law. This is because increasing the amount of gas increases the number of gas particles colliding with the container walls, leading to a higher pressure for the same volume. Conversely, reducing the amount of gas decreases the collision frequency, resulting in lower pressure. Holding the amount of gas constant ensures that the observed pressure changes are solely due to volume variations, allowing for a clean demonstration of the law.
Effect of Changing the Amount of Gas on Pressure-Volume Relationship, What remain constant in boyle’s law
To illustrate the impact of varying the amount of gas, consider a sealed container initially filled with one mole of gas at a specific pressure and volume. If we were to add another mole of gas, keeping the temperature and volume constant, we would observe a significant increase in pressure. This is because the number of gas particles has doubled, leading to a doubling of the collision frequency with the container walls. Conversely, if we were to remove half of the initial gas, the pressure would decrease proportionally because the number of gas particles and thus the collision frequency is reduced.
- Increased Amount of Gas: Pressure increases significantly for a constant volume; the pressure-volume product (PV) increases.
- Decreased Amount of Gas: Pressure decreases significantly for a constant volume; the pressure-volume product (PV) decreases.
- Constant Amount of Gas: Pressure and volume are inversely proportional; the pressure-volume product (PV) remains constant.
Comparison with Non-Constant Gas Amount Situations
Boyle’s Law provides a simplified model applicable only under specific conditions. Real-world scenarios often involve changes in the amount of gas. For example, consider a balloon being inflated. As you add more air (increasing the number of moles), both the pressure and volume of the balloon increase. This situation clearly deviates from Boyle’s Law, where the amount of gas is explicitly held constant. Similarly, the process of a gas leaking from a container would involve a decreasing amount of gas, altering the pressure-volume relationship. These situations necessitate the use of more complex gas laws, such as the Ideal Gas Law (PV = nRT), which accounts for the number of moles (n) and the absolute temperature (T), offering a more comprehensive description of gas behavior. The Ideal Gas Law reduces to Boyle’s Law only when n and T are constant.
Limitations of Boyle’s Law

Boyle’s Law, while a fundamental principle in chemistry, is an idealization. It accurately describes the relationship between pressure and volume of a gas only under specific conditions. Deviations from the law become increasingly significant as we move away from these ideal conditions. Understanding these limitations is crucial for accurate predictions and interpretations in real-world applications.
Boyle’s Law is Most Accurate Under Ideal Conditions
Boyle’s Law holds most accurately for ideal gases at low pressures and moderate temperatures. An ideal gas is a theoretical construct where gas particles are assumed to have negligible volume and no intermolecular forces. At low pressures, the gas molecules are far apart, minimizing intermolecular interactions. Similarly, at moderate temperatures, the kinetic energy of the molecules is sufficient to overcome weak attractive forces. Under these conditions, the pressure-volume relationship closely follows the inverse proportionality described by Boyle’s Law:
PV = k
, where P is pressure, V is volume, and k is a constant.
Deviations from Boyle’s Law at High Pressures and Low Temperatures
At high pressures, the volume of the gas molecules themselves becomes a significant fraction of the total volume. This is because the gas molecules are forced closer together. The assumption of negligible molecular volume in the ideal gas law breaks down, leading to a deviation from the inverse proportionality predicted by Boyle’s Law. The actual volume occupied by the gas is less than what would be predicted by Boyle’s Law.
At low temperatures, intermolecular attractive forces become more significant. As the kinetic energy of the molecules decreases, these attractive forces pull the molecules closer together, reducing the volume. This again causes a deviation from Boyle’s Law. The observed pressure is lower than what would be expected from the ideal gas law because the attractive forces effectively reduce the number of collisions with the container walls. Real gases exhibit a greater compressibility than predicted by Boyle’s Law under these conditions.
Visual Representation of Ideal and Non-Ideal Gas Behavior
Imagine two graphs, both plotting pressure (y-axis) against volume (x-axis). The first graph, representing ideal gas behavior, shows a perfect rectangular hyperbola. As volume decreases, pressure increases proportionally, following the inverse relationship
PV = k
. The curve smoothly approaches both axes but never actually touches them.
The second graph, illustrating non-ideal behavior, shows a similar trend at low pressures and moderate temperatures. However, as pressure increases (or temperature decreases), the curve begins to deviate from the ideal hyperbola. At high pressures, the curve becomes less steep, reflecting the reduced compressibility due to the finite volume of gas molecules. At very low temperatures, the curve might even show an increase in pressure as volume decreases further, illustrating the effect of attractive intermolecular forces dominating over the kinetic energy of the molecules. The deviation from the ideal hyperbola becomes more pronounced as the conditions move further away from the ideal gas approximation.
Applications of Boyle’s Law
Boyle’s Law, describing the inverse relationship between pressure and volume of a gas at constant temperature, finds numerous practical applications across various fields. Understanding this fundamental principle allows for the design and operation of many everyday devices and industrial processes. The consistent predictability of this law makes it a cornerstone of numerous technologies.
Medical Applications
Boyle’s Law is crucial in several medical procedures and devices. The mechanics of breathing, for instance, rely directly on this principle. During inhalation, the diaphragm contracts, increasing the volume of the lungs and thus decreasing the pressure inside. This pressure difference allows air to rush into the lungs. Exhalation is the reverse process. Furthermore, many medical instruments, such as syringes and respiratory equipment, operate based on the principles of Boyle’s Law. For example, the functioning of a syringe involves compressing the plunger (decreasing volume), increasing the pressure inside, and forcing the liquid outwards. Similarly, ventilators use controlled changes in pressure to assist or replace the natural breathing process in patients with respiratory difficulties. The precise control of pressure and volume is vital for effective and safe medical intervention.
Industrial Applications
Boyle’s Law has significant implications in various industrial processes. Pneumatic systems, which utilize compressed air to power tools and machinery, rely heavily on the principle. The compression of air in a pneumatic system increases its pressure, storing potential energy that is then used to perform work. Conversely, the release of compressed air results in expansion and the performance of mechanical work. Furthermore, many industrial processes involving gases, such as filling gas cylinders or controlling gas flow in pipelines, require a precise understanding of Boyle’s Law to ensure safety and efficiency. For instance, the filling of scuba diving tanks involves carefully controlling the pressure and volume of compressed air to maintain safe and usable levels for divers.
Everyday Applications
Beyond medical and industrial applications, Boyle’s Law influences many aspects of daily life. The operation of aerosol cans, for example, utilizes the principle of compressed gas expansion. The pressure inside the can forces the liquid propellant and its contents out when the valve is opened. Similarly, the inflation of balloons and tires depends on the inverse relationship between pressure and volume. As air is pumped into a tire, the volume increases, and consequently, the pressure inside also increases. This increased pressure allows the tire to support the weight of a vehicle. The proper inflation of a tire ensures optimal performance and safety. Even seemingly simple actions like drinking from a straw utilize this principle. The suction action reduces the air pressure inside the straw, creating a pressure difference that draws the liquid upwards.

Tim Redaksi