Introduction to Boyle’s Law: What Remains Constant In The Boyles Law

Boyle’s Law is a fundamental principle in physics describing the inverse relationship between the pressure and volume of a gas, provided the temperature and the amount of gas remain constant. In simpler terms, if you squeeze a gas into a smaller space (decreasing its volume), its pressure will increase. Conversely, if you allow a gas to expand (increasing its volume), its pressure will decrease. This relationship is crucial in understanding the behavior of gases in various applications, from weather balloons to scuba diving equipment.
Boyle’s Law, while now a cornerstone of physics, wasn’t discovered in a single eureka moment. Robert Boyle, an Irish natural philosopher and chemist, meticulously documented his experiments in the mid-17th century. Through a series of careful observations using a J-shaped tube and mercury, he established the inverse proportionality between pressure and volume. His work, published in 1662 in “New Experiments Physico-Mechanicall, Touching the Spring of the Air,” was groundbreaking, providing a quantitative description of gas behavior that laid the foundation for future advancements in thermodynamics and chemistry. The significance of Boyle’s Law extends far beyond its initial application; it represents a paradigm shift in scientific inquiry, highlighting the power of systematic experimentation and mathematical representation in understanding the natural world.
A Simple Experiment Demonstrating Boyle’s Law
A straightforward demonstration of Boyle’s Law can be performed using a syringe and a pressure gauge (or, less precisely, by estimating pressure based on the force required to compress the syringe). Completely fill a standard 60ml syringe with air, ensuring the plunger is fully extended. Seal the tip of the syringe with a small piece of strong tape to prevent air leakage. Attach the pressure gauge to the end of the syringe. Then, systematically compress the plunger to different volumes, recording both the volume and the corresponding pressure reading. Remember to maintain a constant temperature throughout the experiment. It’s crucial to push the plunger slowly to allow the gas to reach equilibrium before taking each measurement. Below is a sample table of potential results. Note that the exact values will depend on the specific equipment used and ambient conditions.
| Pressure (atm) | Volume (L) | Pressure x Volume |
|---|---|---|
| 1.00 | 0.060 | 0.060 |
| 1.20 | 0.050 | 0.060 |
| 1.50 | 0.040 | 0.060 |
| 2.00 | 0.030 | 0.060 |
| 3.00 | 0.020 | 0.060 |
Note that the “Pressure x Volume” column should remain relatively constant, demonstrating the inverse relationship predicted by Boyle’s Law. Small deviations are expected due to experimental error. This simple experiment effectively illustrates the core principle of Boyle’s Law: the product of pressure and volume remains constant at a constant temperature.
Identifying Constants in Boyle’s Law
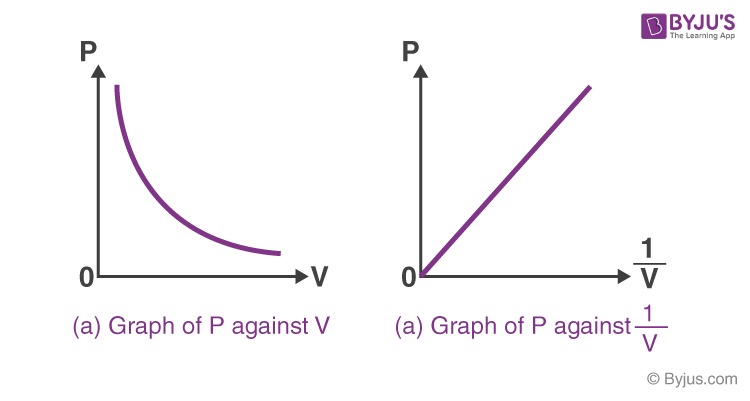
Boyle’s Law, a fundamental principle in gas behavior, describes the inverse relationship between the pressure and volume of a gas at a constant temperature. Understanding the conditions that must remain constant is crucial for accurately applying and interpreting this law. Failure to maintain these constants will lead to deviations from the predicted pressure-volume relationship.
The key constant in Boyle’s Law is temperature. For Boyle’s Law to accurately reflect the relationship between pressure and volume, the temperature of the gas must remain absolutely unchanged throughout the experiment or observation. Any change in temperature will directly influence the kinetic energy of the gas molecules, affecting both pressure and volume independently, thus invalidating the simple inverse relationship. This is because increased temperature leads to increased molecular motion and collisions, resulting in higher pressure for the same volume, or increased volume to maintain the same pressure. Conversely, a decrease in temperature will have the opposite effect.
Temperature’s Impact on Pressure-Volume Relationship
Maintaining a constant temperature is paramount when working with Boyle’s Law. If the temperature fluctuates, the observed relationship between pressure and volume will deviate from the expected inverse proportionality. For example, if we compress a gas and its temperature increases due to the compression (adiabatic process), the observed pressure increase will be greater than predicted by Boyle’s Law alone. Similarly, if a gas expands and cools (also an adiabatic process), the observed pressure decrease will be less than predicted. Therefore, precise temperature control is essential for experimental verification and practical application of Boyle’s Law. This is typically achieved using a thermostatically controlled environment or by performing experiments rapidly enough to minimize any significant temperature changes.
Comparison with Other Gas Laws, What remains constant in the boyles law
Boyle’s Law is one of several gas laws that describe the behavior of ideal gases under specific conditions. Charles’s Law, for instance, focuses on the relationship between volume and temperature at constant pressure, demonstrating a direct proportionality: as temperature increases, volume increases proportionally. Gay-Lussac’s Law similarly explores the relationship between pressure and temperature at constant volume, again showing a direct proportionality: increased temperature leads to increased pressure. Unlike Boyle’s Law which deals with the inverse relationship between pressure and volume at constant temperature, Charles’s and Gay-Lussac’s laws highlight the direct relationships between temperature and either volume (constant pressure) or pressure (constant volume), respectively. The combined gas law integrates all three variables (pressure, volume, and temperature) to describe the behavior of gases under varying conditions, showing how they are interconnected. Each law provides a specific insight into gas behavior under controlled conditions, collectively contributing to a more comprehensive understanding of ideal gas thermodynamics.

Tim Redaksi