The Role of the Amount of Gas: What Stays Constant In The Charles Law
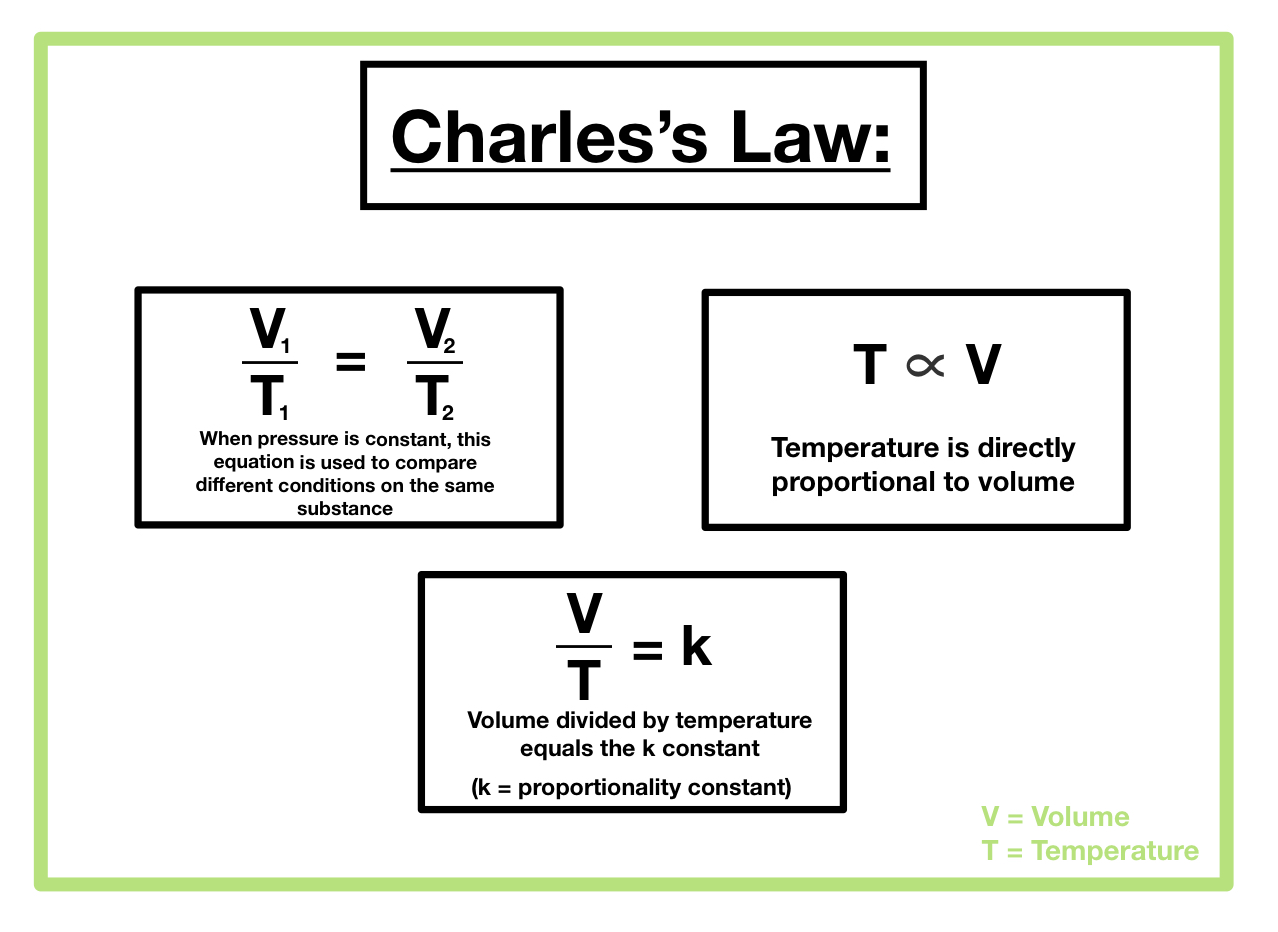
Charles’s Law, which describes the relationship between the volume and temperature of a gas at constant pressure, hinges on a crucial assumption: the amount of gas remains constant. This constancy is not merely a simplifying assumption; it’s fundamental to the law’s validity and predictive power. Understanding the role of the amount of gas is key to applying Charles’s Law correctly and interpreting experimental results.
The amount of gas, typically measured in moles (n), directly impacts the number of gas particles present in a given volume. More gas particles mean more frequent collisions with the container walls, leading to a greater pressure exerted by the gas. If the amount of gas changes while temperature and volume are varied, the pressure will also change, violating the constant pressure condition essential to Charles’s Law. Consequently, the observed relationship between volume and temperature would deviate from the simple proportionality described by the law. The law only holds true when the number of moles of gas remains unchanged throughout the experiment.
Gas Behavior Under Constant Pressure and Varying Amounts of Gas, What stays constant in the charles law
Consider two identical balloons, both initially at room temperature and atmospheric pressure. If we inflate one balloon significantly more than the other, adding a greater number of air molecules, we have increased the amount of gas (n) in that balloon. If we now increase the temperature of both balloons equally, the larger balloon, containing more gas, will expand more than the smaller balloon. This is because the greater number of gas particles in the larger balloon exerts a proportionally greater pressure as temperature rises. To maintain constant pressure, the volume must increase more significantly to accommodate the increased kinetic energy of the more numerous particles. This demonstrates that while Charles’s Law describes a direct proportionality between volume and temperature at *constant* pressure and amount of gas, varying the amount of gas introduces a new variable that complicates the relationship, making the simple V/T = k proportionality invalid. Therefore, maintaining a constant amount of gas is crucial for the accurate application of Charles’s Law.

Tim Redaksi