Introduction to Gas Laws
Gases, unlike solids and liquids, are characterized by their highly compressible nature and their tendency to completely fill any container they occupy. Understanding their behavior is crucial in numerous scientific and engineering applications, from designing efficient engines to predicting weather patterns. Gas laws describe the relationships between the macroscopic properties of gases—pressure, volume, temperature, and amount (moles)—providing a framework for predicting how gases will behave under different conditions.
The behavior of gases is governed by the kinetic molecular theory, which postulates that gases consist of tiny particles in constant, random motion. These particles are assumed to be point masses with negligible volume compared to the volume of the container, and interactions between them are considered negligible except for elastic collisions. These assumptions simplify the description of gas behavior, allowing for the development of relatively simple mathematical relationships.
Historical Development of Gas Laws
The development of gas laws spanned several centuries, with contributions from numerous scientists. Robert Boyle’s experiments in the 17th century established the inverse relationship between pressure and volume at constant temperature (Boyle’s Law). Later, Jacques Charles and Joseph Gay-Lussac independently discovered the direct relationship between volume and temperature at constant pressure (Charles’s Law and Gay-Lussac’s Law). Amedeo Avogadro’s hypothesis, proposed in the early 19th century, stated that equal volumes of gases at the same temperature and pressure contain the same number of molecules, leading to Avogadro’s Law. These individual laws were later combined into the Ideal Gas Law, a more comprehensive equation that relates all four macroscopic properties of a gas. The Ideal Gas Law, while not perfectly accurate for all gases under all conditions, provides a useful approximation for many real-world scenarios.
Real-World Applications of Gas Laws
Gas laws find widespread applications across various fields. In meteorology, understanding the relationship between pressure, temperature, and volume helps predict weather patterns and forecast storms. The design and operation of internal combustion engines rely heavily on the principles of gas laws to optimize fuel efficiency and power output. In the chemical industry, gas laws are essential for controlling and monitoring chemical reactions involving gases, ensuring safe and efficient processes. Furthermore, scuba diving relies on a thorough understanding of gas laws to calculate safe ascent and descent rates to prevent decompression sickness. The inflation of airbags in vehicles is another example, where the rapid expansion of gases upon impact is crucial for passenger safety. Finally, the functioning of many medical devices, such as ventilators and anesthetic delivery systems, depends on a precise control of gas pressure and volume.
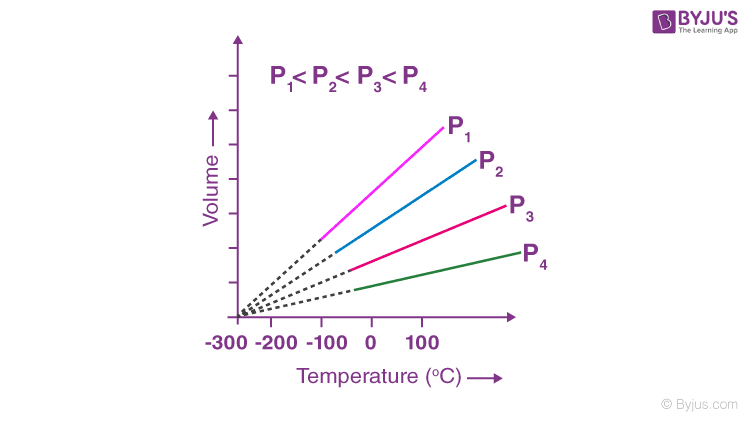
Charles’s Law: Which Law Describes Relationship Between Temperature And Volume

Charles’s Law describes the relationship between the volume and temperature of a gas when the pressure and the amount of gas are held constant. It’s a fundamental gas law that helps us understand how gases behave under varying temperature conditions. This law has numerous applications in various fields, from designing hot air balloons to understanding atmospheric processes.
Statement of Charles’s Law
Charles’s Law states that the volume of a given amount of gas is directly proportional to its absolute temperature, provided the pressure remains constant. This means that if the temperature increases, the volume will increase proportionally, and vice versa. This relationship is particularly useful for predicting gas behavior under different thermal conditions.
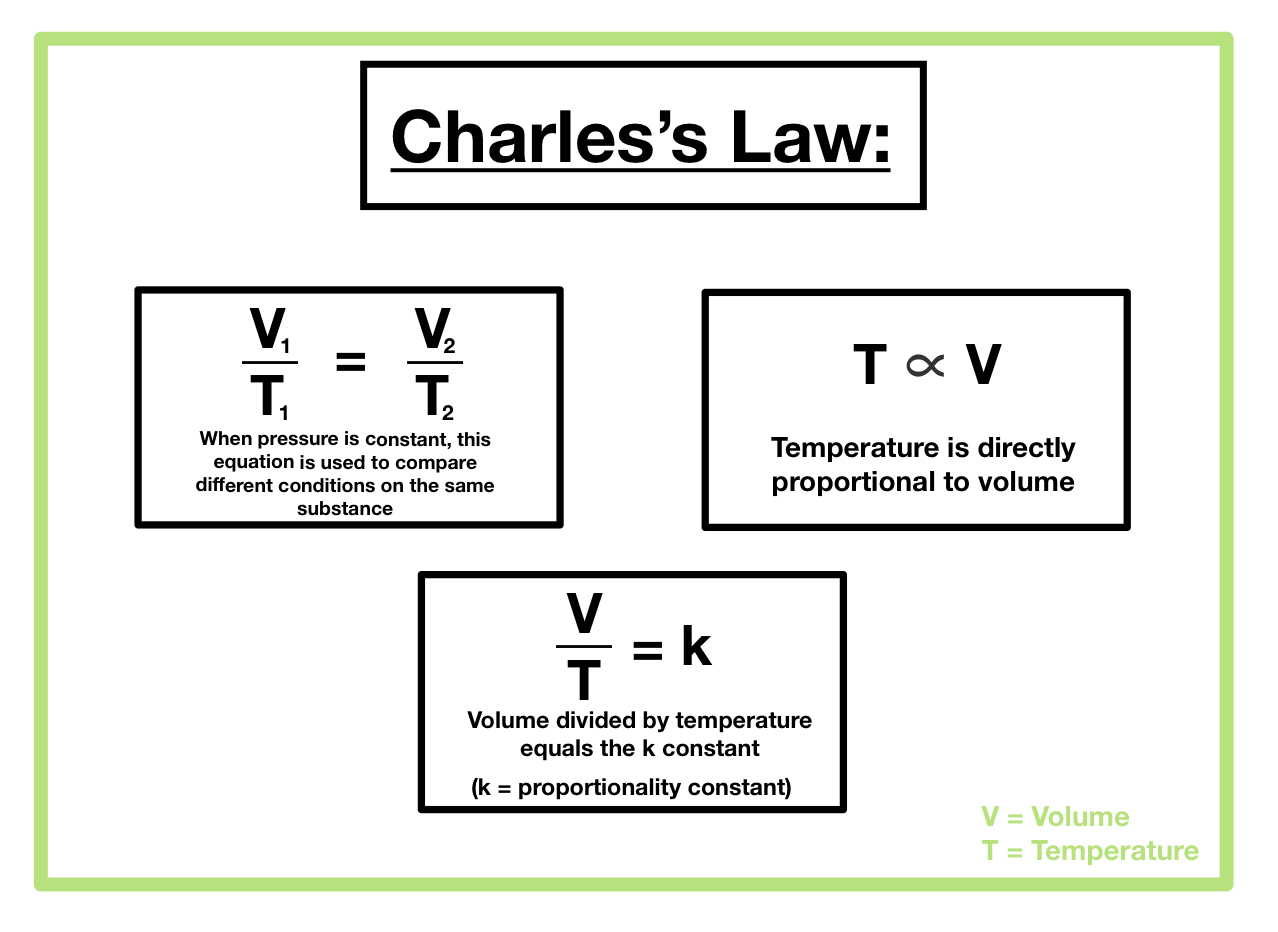
Mathematical Representation of Charles’s Law
Charles’s Law can be mathematically represented as:
V₁/T₁ = V₂/T₂
where:
* V₁ is the initial volume of the gas
* T₁ is the initial absolute temperature of the gas (in Kelvin)
* V₂ is the final volume of the gas
* T₂ is the final absolute temperature of the gas (in Kelvin)
It’s crucial to note that temperature must always be expressed in Kelvin (K) for this equation to be accurate. Converting Celsius to Kelvin is straightforward: K = °C + 273.15.
Conditions for Applicability of Charles’s Law
Charles’s Law is most accurately applied under conditions where the pressure and the amount of gas (number of moles) remain constant. The gas should also ideally behave ideally, meaning that the gas molecules are considered to have negligible volume and no intermolecular forces. Deviations from ideal behavior are more pronounced at high pressures and low temperatures.
Assumptions Made in Deriving Charles’s Law
The derivation of Charles’s Law relies on several key assumptions about the nature of gases: The gas is assumed to be an ideal gas, meaning intermolecular forces are negligible and the volume of the gas molecules themselves is insignificant compared to the total volume. The pressure of the gas remains constant throughout the process. The amount of gas (number of moles) remains constant.
A Simple Experiment Demonstrating Charles’s Law
A simple experiment can be conducted using a balloon and a heat source.
| Experiment Setup | Observation | Data (Temperature and Volume) | Analysis |
|---|---|---|---|
| A partially inflated balloon is placed in a container of ice water (low temperature). The volume of the balloon is measured. | The balloon shrinks in size. | T₁ = 273 K (0°C), V₁ = 100 mL (example) | At lower temperature, the volume of the gas decreases. |
| The same balloon is then placed in a container of warm water (higher temperature). The volume of the balloon is measured again. | The balloon expands in size. | T₂ = 303 K (30°C), V₂ = 110 mL (example) | At higher temperature, the volume of the gas increases. The ratio V₁/T₁ ≈ V₂/T₂ demonstrates Charles’s Law. |
Real Gases and Deviations from Ideal Behavior
The Ideal Gas Law, while a useful simplification, doesn’t perfectly describe the behavior of all gases under all conditions. Real gases, unlike their ideal counterparts, exhibit deviations from this law, particularly at high pressures and low temperatures. Understanding these deviations is crucial for accurate predictions in various applications, from chemical engineering to atmospheric science.
The Ideal Gas Law assumes that gas particles have negligible volume and do not interact with each other. However, real gas molecules do possess a finite volume and experience intermolecular forces (attractive and repulsive). These forces and volumes become increasingly significant as the gas molecules are forced closer together under high pressure or slowed down at low temperatures, leading to deviations from the ideal behavior.
Factors Causing Deviations from Ideal Behavior
The primary factors responsible for the deviations of real gases from ideal behavior are intermolecular forces and the finite volume occupied by gas molecules. At high pressures, the volume occupied by the gas molecules themselves becomes a significant fraction of the total volume, leading to a larger measured volume than predicted by the Ideal Gas Law. Simultaneously, at low temperatures, the kinetic energy of the molecules decreases, allowing the attractive intermolecular forces to become more prominent. These forces cause the molecules to clump together, resulting in a lower pressure than predicted by the Ideal Gas Law. The combined effect of these factors leads to significant deviations, especially at conditions far from ideal.
Examples of Real Gas Behavior
Carbon dioxide (CO2) is a good example of a real gas that deviates significantly from ideal behavior. At low temperatures and high pressures, the attractive forces between CO2 molecules become dominant, leading to liquefaction or even solidification. Conversely, at high temperatures and low pressures, the gas behaves more ideally as the kinetic energy overcomes the intermolecular forces. Similarly, gases like methane (CH4) and ammonia (NH3) show deviations due to their respective intermolecular forces, with ammonia exhibiting stronger deviations than methane due to its stronger hydrogen bonding.
Real Gases and Their Deviations, Which law describes relationship between temperature and volume
The following list illustrates how several real gases deviate from ideal gas behavior under high pressure and low temperature conditions. Note that the extent of deviation varies depending on the specific gas and the severity of the conditions.
- Carbon Dioxide (CO2): Under high pressure and low temperature, CO2 deviates significantly due to strong intermolecular forces leading to liquefaction or even sublimation (solid to gas). The volume occupied by the CO2 molecules becomes considerable at high pressure.
- Ammonia (NH3): Ammonia exhibits substantial deviations due to strong hydrogen bonding between molecules. At low temperatures, these bonds become highly significant, causing greater deviations than predicted by the ideal gas law. High pressure further exacerbates the deviation by reducing the intermolecular distance.
- Methane (CH4): Methane shows noticeable deviations, though less pronounced than ammonia or carbon dioxide, due to weaker van der Waals forces. At high pressures, the volume of the methane molecules becomes a more significant factor.
- Water Vapor (H2O): Water vapor, particularly at lower temperatures, displays significant deviations from ideal behavior due to strong hydrogen bonding. High pressure further compresses the molecules, increasing the impact of these intermolecular forces.

Tim Redaksi