Which Physics Law Explains Gun Recoil?

Conservation of Momentum

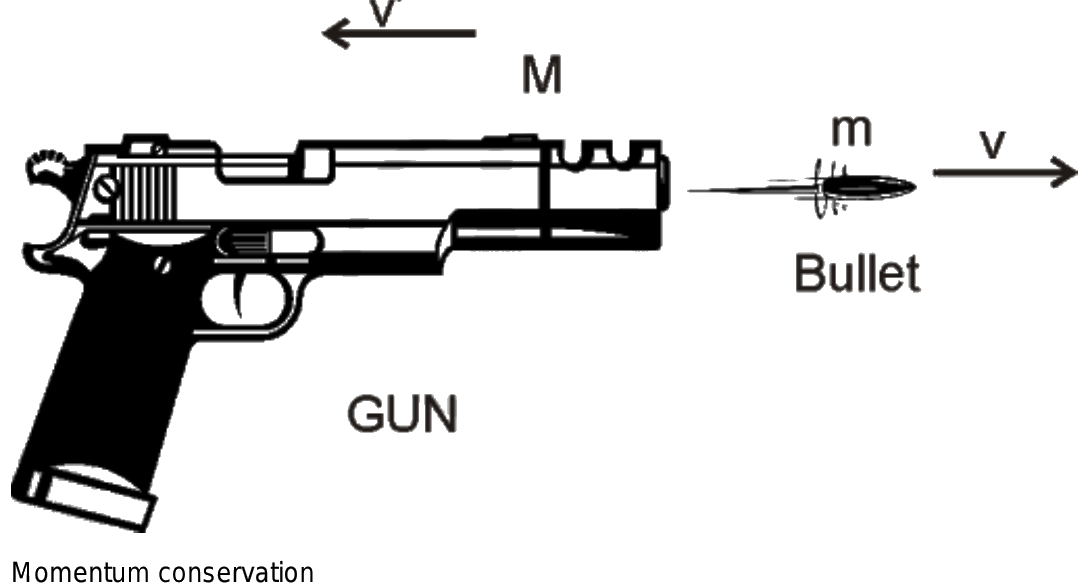
The recoil of a firearm is a direct consequence of the principle of conservation of momentum. This fundamental law of physics states that the total momentum of a closed system remains constant if no external forces act on it. In the context of a gun firing, the system comprises the gun and the bullet. Before firing, the total momentum is zero, as both the gun and the bullet are at rest. After firing, the momentum of the bullet in one direction is balanced by the momentum of the gun in the opposite direction, maintaining a net momentum of zero.

The recoil experienced by the shooter is a manifestation of this momentum conservation. The bullet, having a relatively small mass, is propelled forward at a high velocity. To maintain the total momentum of the system at zero, the gun, with a significantly larger mass, moves backward with a lower velocity. This backward movement is what we perceive as recoil.

Momentum Before and After Firing

Before the gun is fired, both the bullet and the gun are stationary. Therefore, their individual momenta are zero, and the total momentum of the system (gun + bullet) is also zero. After the firing, the bullet possesses a significant forward momentum (mass of bullet x velocity of bullet), and to compensate, the gun acquires an equal and opposite momentum (mass of gun x recoil velocity). This ensures the total momentum of the system remains zero, in accordance with the law of conservation of momentum.

Mass and Velocity’s Influence on Recoil

The mass and velocity of both the bullet and the gun are crucial factors determining the magnitude of the recoil. A heavier bullet, fired at the same velocity as a lighter bullet, will impart a greater momentum to the bullet and, consequently, a greater recoil to the gun. Similarly, a higher bullet velocity, even with the same bullet mass, will increase the bullet’s momentum and thus the gun’s recoil. Conversely, a heavier gun will experience less recoil than a lighter gun when firing the same bullet, as the same momentum is distributed across a larger mass, resulting in a lower recoil velocity.

Mathematical Model of Recoil

The relationship between the bullet’s mass (m_b), bullet’s velocity (v_b), gun’s mass (m_g), and the gun’s recoil velocity (v_g) can be expressed mathematically using the principle of conservation of momentum:

m_bv_b + m_gv_g = 0

This equation states that the total momentum before firing (zero) equals the total momentum after firing. Solving for the recoil velocity (v_g), we get:

v_g = – (m_bv_b) / m_g

The negative sign indicates that the recoil velocity is in the opposite direction to the bullet’s velocity.

Calculating Recoil Velocity

Calculating the recoil velocity involves these steps:

1. Determine the mass of the bullet (m_b) and the gun (m_g). This information is typically provided by the manufacturer or can be measured directly.
2. Measure or obtain the muzzle velocity of the bullet (v_b). This is often specified by the manufacturer or can be determined using a chronograph.
3. Substitute the values of m_b, v_b, and m_g into the equation: v_g = – (m_bv_b) / m_g
4. Calculate the recoil velocity (v_g). The result will be a negative value, indicating the direction of the recoil is opposite to the bullet’s direction. The magnitude of this value represents the speed of the gun’s recoil.

For example, consider a 10g bullet (0.01kg) fired from a 2kg gun at a velocity of 500 m/s. The recoil velocity would be: v_g = – (0.01 kg * 500 m/s) / 2 kg = -2.5 m/s. This means the gun recoils at 2.5 m/s in the opposite direction of the bullet.

Illustrative Examples: Which Pysics Law Explains Why A Gun Kicks When Fired

Understanding recoil in firearms requires visualizing the forces at play. The following examples illustrate how mass, design, and force vectors influence the recoil experience.

Let’s explore how different firearm characteristics affect recoil, keeping in mind that conservation of momentum is the underlying principle.

Heavier Guns and Reduced Recoil

A heavier gun experiences less recoil than a lighter gun when firing the same ammunition because the heavier mass increases the denominator in the momentum equation (momentum = mass x velocity). Consider two scenarios: A 5kg rifle fires a 0.01kg bullet at 800 m/s. The rifle’s recoil velocity can be calculated using the conservation of momentum: (mass of rifle * recoil velocity) = -(mass of bullet * bullet velocity). Therefore, the recoil velocity of the 5kg rifle is approximately -1.6 m/s. Now, imagine a 2kg rifle firing the same bullet. Its recoil velocity would be approximately -4 m/s. The negative sign indicates the opposite direction of the bullet. The heavier rifle has a significantly lower recoil velocity, making it more comfortable to shoot.

Recoil Angle and Force Vectors

The angle of recoil isn’t always directly backward. The design of the firearm, specifically the position of the barrel relative to the shooter’s shoulder and the presence of features like muzzle brakes, significantly influences the recoil vector. If the barrel is not perfectly aligned with the shooter’s shoulder, the recoil force will be directed at an angle. A muzzle brake redirects some of the propellant gases to the side, reducing the backward force and thus altering the recoil angle. For instance, a shotgun with a significant upward barrel angle might exhibit a more pronounced upward recoil. This is because the force vector is not simply a linear backward push; it’s a combination of forces, which are influenced by the geometry of the firearm and the gases’ ejection.

Gun Design and Recoil Mitigation, Which pysics law explains why a gun kicks when fired

Several design features effectively mitigate recoil. The stock of the gun, for example, is crucial. A well-designed stock, fitted to the shooter’s shoulder, distributes the recoil force across a larger area, reducing the felt recoil. The stock’s material and design (e.g., rubber buttpad) also absorb some of the impact. Muzzle brakes, as mentioned earlier, redirect propellant gases to the side and downwards, further decreasing felt recoil by reducing the rearward force. Recoil reducers, often integrated into the gun’s mechanism, use mechanical means (like springs or dampeners) to slow down the gun’s backward movement.

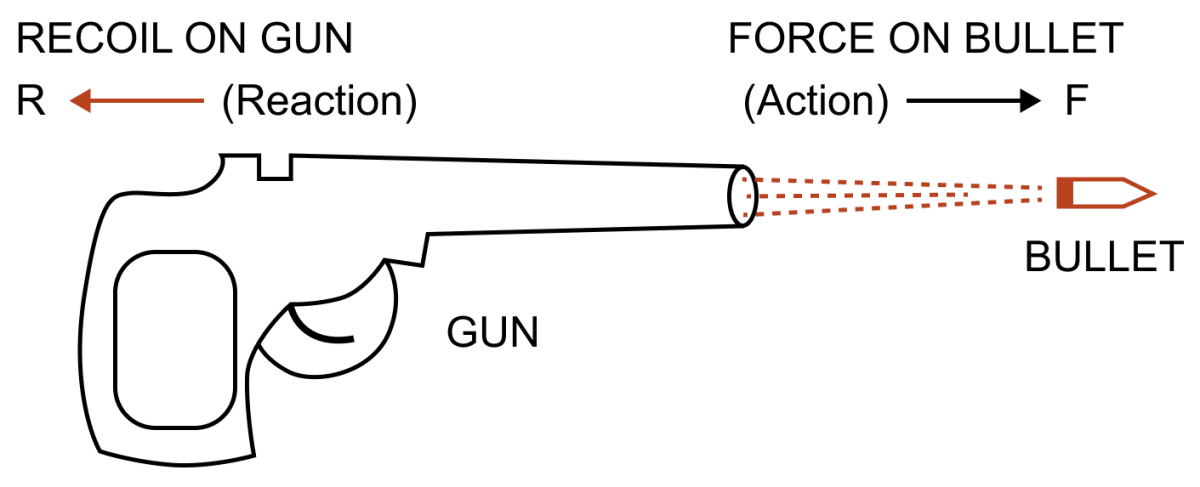
Forces Acting on Bullet and Gun During Firing

Imagine a simplified illustration: A rectangle represents the gun, and a smaller rectangle, the bullet, sits inside the barrel. A large, bold arrow labeled “Propellant Gas Pressure” points from the rear of the bullet toward the muzzle. This force pushes both the bullet and the gun. Another arrow, labeled “Bullet Force,” points to the right (assuming the gun is pointed to the right), representing the force exerted by the expanding gases on the bullet, propelling it forward. Simultaneously, an arrow labeled “Recoil Force,” points to the left, representing the equal and opposite force acting on the gun. This recoil force pushes the gun backward, with its magnitude directly proportional to the bullet’s momentum, as dictated by the conservation of momentum. The size and length of these arrows visually represent the magnitude of each force, with the “Bullet Force” and “Recoil Force” being equal and opposite in magnitude. The “Propellant Gas Pressure” arrow illustrates the source of the initial energy that sets the whole process in motion.